江苏省泰州市兴化市2018届九年级上学期数学期中考试试卷
试卷更新日期:2018-12-21 类型:期中考试
一、单选题
-
1. 数据60,70,40,30这四个数的平均数是( )A、40 B、50 C、60 D、702. 若关于x的函数y=(2﹣a)x2﹣x是二次函数,则a的取值范围是( )A、a≠0 B、a≠2 C、a<2 D、a>23. 一个布袋里装有2个红球,3个黑球,4个白球,它们除颜色外都相同,从中任意摸出1个球,则下事件中,发生的可能性最大的是( )A、摸出的是白球 B、摸出的是黑球 C、摸出的是红球 D、摸出的是绿球4. 下列说法正确的是( )A、三点确定一个圆 B、和半径垂直的直线是圆的切线 C、一个三角形只有一个外接圆 D、三角形的内心到三角形三个顶点的距离相等5. 关于抛物线 ,下列说法错误的是( )A、开口向上 B、与x轴有且只有一个公共点 C、对称轴是直线
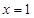 D、当x>0时,y随x的增大而增大
6. 如图, A,B,C三点在⊙O上,若∠BAC=36°,⊙O的半径为1,则劣弧BC的长是( )
D、当x>0时,y随x的增大而增大
6. 如图, A,B,C三点在⊙O上,若∠BAC=36°,⊙O的半径为1,则劣弧BC的长是( ) A、
A、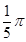 B、
B、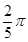 C、
C、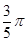 D、
D、
二、填空题
-
7. 某班共有6名学生干部,其中4名是男生,2名是女生,任意抽一名学生干部去参加一项活动,恰好是男生的概率是.8. 已知一组数据为:12,9,10,8,1l,则这组数据的方差是.9. 二次函数 、 的图象如图所示,则mn(填“>”或“<”).
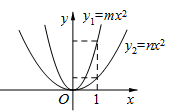 10. 如图,一块飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 .
10. 如图,一块飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 . 11. 如图,直角坐标系中一条圆弧经过网格点A、B、C,其中,B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 .
11. 如图,直角坐标系中一条圆弧经过网格点A、B、C,其中,B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 .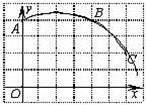 12. 如图,⊙O与正五边形ABCDE的两边AE、CD分别相切于A、C两点,则∠AOC的度数为 .
12. 如图,⊙O与正五边形ABCDE的两边AE、CD分别相切于A、C两点,则∠AOC的度数为 .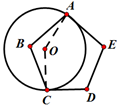 13. 把抛物线 沿x轴向左平移4个单位,再沿y轴向上平移3个单位后,所得新抛物线相应的函数表达式是.14. 给一个圆锥形零件的侧面涂漆,零件的尺寸要求如图所示,则需要涂漆的面积为 (结果保留π).
13. 把抛物线 沿x轴向左平移4个单位,再沿y轴向上平移3个单位后,所得新抛物线相应的函数表达式是.14. 给一个圆锥形零件的侧面涂漆,零件的尺寸要求如图所示,则需要涂漆的面积为 (结果保留π).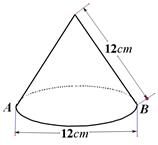 15. 如图,直线y =mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是 .
15. 如图,直线y =mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是 .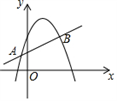 16. 如图,⊙O是正方形ABCD的外接圆,AB=2,点E是劣弧AD上任意一点,CF⊥BE于F. 当点E从点A出发按顺时针方向运动到点D时,则AF的取值范围是.
16. 如图,⊙O是正方形ABCD的外接圆,AB=2,点E是劣弧AD上任意一点,CF⊥BE于F. 当点E从点A出发按顺时针方向运动到点D时,则AF的取值范围是.
三、解答题
-
17.(1)、已知二次函数 的图象经过点(﹣2,8)和(﹣1,5),求这个二次函数的表达式;(2)、已知抛物线的顶点为(﹣1,﹣3),与y轴的交点为(0,﹣5),求这个抛物线相应的函数表达式.18. 为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级
平均分
中位数
众数
方差
八(1)
85
b
c
22.8
八(2)
a
85
85
19.2
(1)、直接写出表中a,b,c的值;
(2)、根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.19. 某校九年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计分析,绘制了如下不完整的统计表和统计图(图).次数
10
8
6
5
人数
3
a
2
1
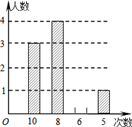 (1)、表中a=;(2)、请将条形统计图补充完整;(3)、从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?20. 从甲、乙、丙、丁4名选手中随机抽取两名选手参加乒乓球比赛,请用画树状图或列表的方法列出所有可能的结果,并求甲、乙两名选手恰好被抽到的概率.21. 在直径为1000毫米的圆柱形油罐内装进一些油.其横截面如图.油面宽AB=600毫米.
(1)、表中a=;(2)、请将条形统计图补充完整;(3)、从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?20. 从甲、乙、丙、丁4名选手中随机抽取两名选手参加乒乓球比赛,请用画树状图或列表的方法列出所有可能的结果,并求甲、乙两名选手恰好被抽到的概率.21. 在直径为1000毫米的圆柱形油罐内装进一些油.其横截面如图.油面宽AB=600毫米.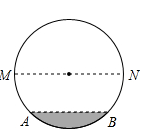 (1)、求油的最大深度;(2)、如果再注入一些油后,油面宽变为800毫米,此时油面上升了多少毫米?22. 已知二次函数 .(1)、求证:无论m为任何实数,此函数图象与x轴总有两个交点;(2)、若此函数图象与x轴的一个交点为(-3,0),求此函数图象与x轴的另一个交点坐标.23. 如图,E是△ABC的内心,AE的延长线交△ABC的外接圆于点D.
(1)、求油的最大深度;(2)、如果再注入一些油后,油面宽变为800毫米,此时油面上升了多少毫米?22. 已知二次函数 .(1)、求证:无论m为任何实数,此函数图象与x轴总有两个交点;(2)、若此函数图象与x轴的一个交点为(-3,0),求此函数图象与x轴的另一个交点坐标.23. 如图,E是△ABC的内心,AE的延长线交△ABC的外接圆于点D. (1)、BD与DE相等吗?为什么?(2)、若∠BAC=90°,DE=4,求△ABC外接圆的半径.24. 如图,AB是⊙O的直径,弦AD平分∠BAC,DE⊥AC交AC的延长线于点E.
(1)、BD与DE相等吗?为什么?(2)、若∠BAC=90°,DE=4,求△ABC外接圆的半径.24. 如图,AB是⊙O的直径,弦AD平分∠BAC,DE⊥AC交AC的延长线于点E. (1)、求证:DE是⊙O的切线;(2)、若AD=BC,⊙O半径为6,求∠CAD与 围成的阴影部分的面积.25. 如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(2,8),且与x轴相切于点B.
(1)、求证:DE是⊙O的切线;(2)、若AD=BC,⊙O半径为6,求∠CAD与 围成的阴影部分的面积.25. 如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(2,8),且与x轴相切于点B. 图①
图①  图②(1)、当x>0,y=5时,求x的值;(2)、当x = 6时,求⊙P的半径;(3)、求y关于x的函数表达式,请判断此函数图象的形状,并在图②中画出此函数的图象(不必列表,画草图即可).26. 如图,已知二次函数 的图象经过点C(0,3),与 轴分别交于点A、点B(3,0).点 、 、 都在这个二次函数的图象上,其中0< <4,连接DE、DF、EF,记△DEF的面积为S.
图②(1)、当x>0,y=5时,求x的值;(2)、当x = 6时,求⊙P的半径;(3)、求y关于x的函数表达式,请判断此函数图象的形状,并在图②中画出此函数的图象(不必列表,画草图即可).26. 如图,已知二次函数 的图象经过点C(0,3),与 轴分别交于点A、点B(3,0).点 、 、 都在这个二次函数的图象上,其中0< <4,连接DE、DF、EF,记△DEF的面积为S.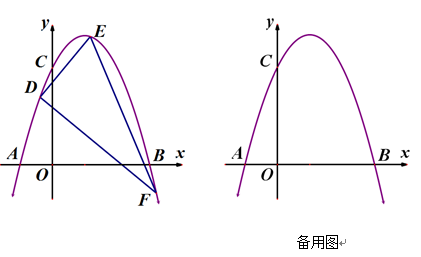 (1)、求二次函数 的表达式;(2)、若 =0,求S的最大值,并求此时 的值;(3)、若 =2,当 取不同数值时,S的值是否变化,如不变,求该定值;如变化,试用含 的代数式表示S.
(1)、求二次函数 的表达式;(2)、若 =0,求S的最大值,并求此时 的值;(3)、若 =2,当 取不同数值时,S的值是否变化,如不变,求该定值;如变化,试用含 的代数式表示S.