江苏省泰兴市黄桥东区域2019届九年级上学期数学期中考试试卷
试卷更新日期:2018-12-21 类型:期中考试
一、单选题
-
1. 比例尺为1:800的学校地图上,某条路的长度约为5cm,它的实际长度约为( )A、400cm B、40m C、200cm D、20m2. 如果 ( ),那么下列比例式中正确的是( )A、
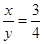 B、
B、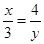 C、
C、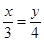 D、
D、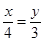 3. 在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球,从中任意摸出一个球,则摸出白球的概率是( )A、 B、 C、
3. 在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球,从中任意摸出一个球,则摸出白球的概率是( )A、 B、 C、 D、
4. 如图,在△ABC中,D,E分别是AB,AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:AB=( )
D、
4. 如图,在△ABC中,D,E分别是AB,AC上的点,且DE∥BC,若S△ADE:S△ABC=4:9,则AD:AB=( )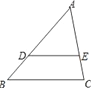 A、1:2 B、2:1 C、2:3 D、1:35. 若一组数据2、4、6、8、x的方差比另一组数据5、7、9、11、13的方差大,则 x 的值可以是( )A、12 B、10 C、2 D、06. 在△ABC中,AB=AC,AD⊥BC,中线CE交AD于点F,AD=18,EF=5,则BC长为( )
A、1:2 B、2:1 C、2:3 D、1:35. 若一组数据2、4、6、8、x的方差比另一组数据5、7、9、11、13的方差大,则 x 的值可以是( )A、12 B、10 C、2 D、06. 在△ABC中,AB=AC,AD⊥BC,中线CE交AD于点F,AD=18,EF=5,则BC长为( )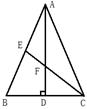 A、12 B、14 C、16 D、18
A、12 B、14 C、16 D、18二、填空题
-
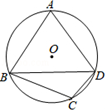
7. 一组数据﹣3,﹣2,0,1,2,3的极差是.8. 若关于x的一元二次方程x2-2x+a-1=0有两个相等实数根,则a = .9. 已知线段a、b、c,其中c是a、b的比例中项,若a =9cm,b=4cm,则线段c=.10. 若圆O的半径是5,圆心的坐标是(0,0),点P的坐标是(-4,3),则点P与⊙O的位置关系是 .11. 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°,则∠ABD=°.
 12. 圆心角是60°,半径为2的扇形的弧长等于.13. 如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是 .
12. 圆心角是60°,半径为2的扇形的弧长等于.13. 如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是 .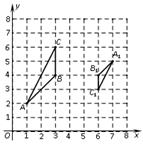 14. 如图,某种鱼缸的主视图可视为弓形,该鱼缸装满水时的最大深度CD为18cm,半径OC为13cm,则鱼缸口的直径AB= cm.
14. 如图,某种鱼缸的主视图可视为弓形,该鱼缸装满水时的最大深度CD为18cm,半径OC为13cm,则鱼缸口的直径AB= cm.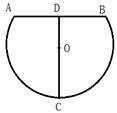 15. 在Rt△ABC中,∠ACB=90º,AC=8,BC=6,点D、E分别在AC、AB上,且△ADE是直角三角形,△BDE是等腰三角形,则BE=.
15. 在Rt△ABC中,∠ACB=90º,AC=8,BC=6,点D、E分别在AC、AB上,且△ADE是直角三角形,△BDE是等腰三角形,则BE=.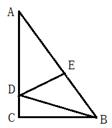 16. 如图,在等腰
16. 如图,在等腰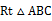 中,
中, 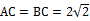 ,点
,点 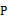 在以斜边
在以斜边 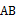 为直径的半圆上,
为直径的半圆上, 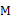 为
为 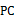 的中点.当点
的中点.当点 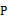 沿半圆从点
沿半圆从点  运动至点
运动至点 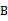 时,点
时,点 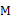 运动的路径长是 .
运动的路径长是 . 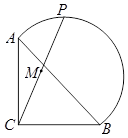
三、解答题
-
17. 解方程(1)、(2)、x(3-2x)= 4 x-618. 已知关于x的一元二次方程x2﹣(4m+1)x+3m2+m=0.(1)、求证:无论m取何实数时,原方程总有两个实数根;(2)、若原方程的两个实数根之和大于0,求m的取值范围.19. 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:


根据以上信息,整理分析数据如下:
 (1)、写出表格中a,b,c的值;(2)、分别运用上表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?20. 初三(1)班要从甲、乙、丙、丁这 名同学中随机选取 名同学参加学校毕业生代表座谈会.
(1)、写出表格中a,b,c的值;(2)、分别运用上表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?20. 初三(1)班要从甲、乙、丙、丁这 名同学中随机选取 名同学参加学校毕业生代表座谈会.
(1)、已确定甲参加,则另外1人恰好选中乙的概率是;
(2)、随机选取2名同学,用树状图或列表求出恰好选中甲和乙的概率.
21. 如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作: (1)、利用网格图确定该圆弧所在圆的圆心D的位置(保留画图痕迹);(2)、连接AD、CD,则⊙D的半径为(结果保留根号),∠ADC的度数为;(3)、若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).22. 如图,在⊙O中,AB是⊙O的弦,CD是⊙O的直径,且AB⊥CD,垂足为G,点E在劣弧 上,连接CE.
(1)、利用网格图确定该圆弧所在圆的圆心D的位置(保留画图痕迹);(2)、连接AD、CD,则⊙D的半径为(结果保留根号),∠ADC的度数为;(3)、若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).22. 如图,在⊙O中,AB是⊙O的弦,CD是⊙O的直径,且AB⊥CD,垂足为G,点E在劣弧 上,连接CE.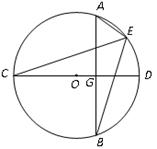 (1)、求证CE平分∠AEB;(2)、连接BC,若BC∥AE,且CG=4,AB=6,求BE的长.23. 某批发商以20元/千克的价格购入了某种水果100千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=30+2x,但保存这批水果平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批水果每天还需20元的费用.(1)、若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为(元/千克),获得的总利润为(元);(2)、设批发商在保存了x天后一次性卖出了保存水果,获得了200元的利润,求这批水果的保存时间.24. 如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.
(1)、求证CE平分∠AEB;(2)、连接BC,若BC∥AE,且CG=4,AB=6,求BE的长.23. 某批发商以20元/千克的价格购入了某种水果100千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=30+2x,但保存这批水果平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批水果每天还需20元的费用.(1)、若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为(元/千克),获得的总利润为(元);(2)、设批发商在保存了x天后一次性卖出了保存水果,获得了200元的利润,求这批水果的保存时间.24. 如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.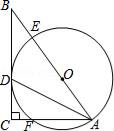 (1)、判断直线BC与⊙O的位置关系并证明;(2)、若⊙O的半径为2,AC=3,求BD的长度.25. 如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(不与O、C重合),作AF⊥BE,垂足为G,分别交BC、OB于F、H,连接OG、CG.
(1)、判断直线BC与⊙O的位置关系并证明;(2)、若⊙O的半径为2,AC=3,求BD的长度.25. 如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(不与O、C重合),作AF⊥BE,垂足为G,分别交BC、OB于F、H,连接OG、CG.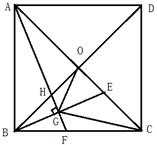 (1)、求证:AH=BE;(2)、∠AGO的度数是否为定值?说明理由;(3)、若∠OGC=90°,BG= ,求△OGC的面积.26. 已知:a、b、c均为非零实数,且a>b>c,关于x的一元二次方程 (a≠0)其中一个实数根为2。(1)、填空:4a+2b+c0,a0,c0(填“>”,“<”或“=”);(2)、若关于x的一元二次方程 (a≠0)的两个实数根,满足一个根为另一个根的2倍,我们就称这样的方程为“倍根方程”,若原方程是倍根方程,则求a、c之间的关系。(3)、若a=1时,设方程的另一根为m(m≠2),在两根之间(不包含两根)的所有整数的绝对值之和是7,求b的取值范围.
(1)、求证:AH=BE;(2)、∠AGO的度数是否为定值?说明理由;(3)、若∠OGC=90°,BG= ,求△OGC的面积.26. 已知:a、b、c均为非零实数,且a>b>c,关于x的一元二次方程 (a≠0)其中一个实数根为2。(1)、填空:4a+2b+c0,a0,c0(填“>”,“<”或“=”);(2)、若关于x的一元二次方程 (a≠0)的两个实数根,满足一个根为另一个根的2倍,我们就称这样的方程为“倍根方程”,若原方程是倍根方程,则求a、c之间的关系。(3)、若a=1时,设方程的另一根为m(m≠2),在两根之间(不包含两根)的所有整数的绝对值之和是7,求b的取值范围.