江苏省盐城市大丰区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2018-12-21 类型：期中考试
一、单选题
-
1. 在下列黑体大写英文字母中，不是轴对称图形的是（ ）A、E B、M C、N D、H2. 下列各组数中，是勾股数的是（ ）A、2、3、4 B、3、4、5 C、4、5、6 D、5、6、73. 下列各条件中，能判定两个三角形全等的是（ ）A、两角一边对应相等 B、两边一角对应相等 C、两个直角三角形的锐角都对应相等 D、两边对应相等4. 64的算术平方根是（ ）A、－8 B、8 C、－8或8 D、45. 如果一个三角形的一条边的平方等于另外两条边的平方差，则此三角形是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法判断6. 如图，小雅家(图中点O处)门前有一条东西走向的公路，经测量得知有一水塔(图中点A处)在她家北偏东60度500 m处，那么水塔所在的位置到公路的距离AB是（ ）
A、250 m B、 250
m
C、
m
D、 250 
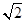m
二、填空题
-
7. 小红从旗台出发向正北方向走6米，接着向正东方向走8米，现在她离旗台的距离是米．8. 1的立方根是 ．9. 角是轴对称图形，它的对称轴是 ．10. 小刚的体重为43.05 kg，将43.05 kg精确到0.1 kg是kg．11. 如图，数轴上的点A，B，O，C，D分别表示数﹣2、﹣1、0、1、2，则表示数 的点应落在相邻两点之间．
12. 如图，已知方格纸中是 个相同的正方形，则 度.
13. 已知直角三角形的直角边分别为5和12，则斜边上的中线为 ．14. 如图，△ABC≌△ADE，∠B=80°，∠C=30°，∠DAC=25°，则∠EAC的度数= ．
15. 如图，在△ABC中，DE是BC的垂直平分线．若AB+AC=8，则△ACE的周长是 ．
16. 已知等边△ABC的高为6，在这个三角形所在的平面内有一点P，若点P到直线AB的距离是1，点P到直线AC的距离是3，则点P到直线BC的距离可能是 ．
三、解答题
-
17.(1)、求x的值：8x3=27(2)、计算：18. 利用网格线作图：在BC上找一点P，使点P到AB和AC的距离相等．然后，在射线AP上找一点Q，使QB=QC．
19. 如图，某住宅小区在施工过程中留下了一块空地（图中的四边形ABCD），经测量，在四边形ABCD中，AB=3m，BC=4m，CD=12m，DA=13m，∠B=900 ． 小区为美化环境，欲在空地上铺草坪，已知草坪每平方米100元，试问铺满这块空地共需花费多少元？
20. 已知正数x的两个平方根分别为3﹣a和2a+7．(1)、求a的值；(2)、求44﹣x这个数的立方根．21. 已知：如图，A、C、F、D在同一直线上，AF＝DC，AB∥DE，AB＝DE.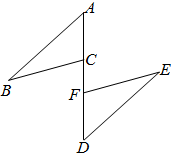
求证：
(1)、△ABC≌△DEF；(2)、BC∥EF.22. 如图，△ABC中，AB=AC=5，AB的垂直平分线DE交AB、AC于E、D．
(1)、若△BCD的周长为8，求BC的长；(2)、若∠A=40°，求∠DBC的度数．23. 在△ABC中，AB=AC，D为AC的中点，DE⊥AB于点E，DF⊥BC于点F，且DE=DF．
(1)、求证：△ADE≌△CDF；(2)、求证：△ABC是等边三角形．24. 如图，在△ABC中，AB=CB，∠ABC=∠90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连接AE、DE、DC．
(1)、求证：△ABE≌△CBD；(2)、若∠CAE=30°，求∠EDC的度数．25. 数学课上，张老师举了下面的例题：例1 等腰三角形 中， ，求 的度数.（答案： ）
例2 等腰三角形 中， ，求 的度数.（答案： 或 或 ）
张老师启发同学们进行变式，小敏编了如下一题：
变式 等腰三角形 中， ，求 的度数.
(1)、请你解答以上的变式题.(2)、解（1）后，小敏发现， 的度数不同，得到 的度数的个数也可能不同.如果在等腰三角形 中，设 ，当 有三个不同的度数时，请你探索 的取值范围.26. △ABC和△ECD都是等边三角形
(1)、如图1，若B、C、D三点在一条直线上，求证：BE=AD；(2)、保持△ABC不动，将△ECD绕点C顺时针旋转，使∠ACE=90°（如图2），BC与DE有怎样的位置关系？说明理由．27. 如图，在长方形ABCD中，AB=CD=6cm，BC=10cm，点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒：
(1)、PC=cm．（用t的代数式表示）(2)、当t为何值时，△ABP≌△DCP？(3)、当点P从点B开始运动，同时，点Q从点C出发，以v cm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由．