辽宁省大连市旅顺口区2018-2019学年高一上学期数学期中考试试卷
试卷更新日期:2018-12-19 类型:期中考试
一、单选题
-
1. 已知集合 ,则 ( )A、
 B、
B、 C、
C、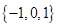 D、
D、 2. 下列函数中,既是偶函数又在区间 上单调递减的是( )A、
2. 下列函数中,既是偶函数又在区间 上单调递减的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列四个命题中的真命题是( )A、∀x∈R,x2+3<0 B、∀x∈N,x2>1 C、∃x∈Z,使
3. 下列四个命题中的真命题是( )A、∀x∈R,x2+3<0 B、∀x∈N,x2>1 C、∃x∈Z,使 D、∃x∈Q,x2=3
4. 已知集合 ,若 中只有一个元素,则 的值是( )A、0 B、
D、∃x∈Q,x2=3
4. 已知集合 ,若 中只有一个元素,则 的值是( )A、0 B、 C、0 或
C、0 或  D、0 或
D、0 或 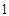 5. 下列四组函数中,表示同一函数的是( ).A、
5. 下列四组函数中,表示同一函数的是( ).A、 B、
B、 C、
C、 D、
D、 ,
,  6. 已知函数 的定义域为 , 的定义域为( )A、
6. 已知函数 的定义域为 , 的定义域为( )A、 B、
B、 C、
C、 D、
D、 7. 已知 ,则 ( )A、36 B、26 C、16 D、48. 已知函数 ,在下列区间中,函数 存在零点的是( )A、
7. 已知 ,则 ( )A、36 B、26 C、16 D、48. 已知函数 ,在下列区间中,函数 存在零点的是( )A、 B、
B、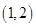 C、
C、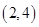 D、
D、 9. 下列叙述中正确的是( )A、若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” B、若a,b,c∈R,则“ab2>cb2”的充要条件是“a>c” C、命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0” D、若p:x<3,q:-110. 已知函数 ,则 的值是( )A、2 B、3 C、5 D、711. 函数 的图象大致为( )A、
9. 下列叙述中正确的是( )A、若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” B、若a,b,c∈R,则“ab2>cb2”的充要条件是“a>c” C、命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0” D、若p:x<3,q:-110. 已知函数 ,则 的值是( )A、2 B、3 C、5 D、711. 函数 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 12. 若对于任意 ,都有 成立,则 的范围是( )A、
12. 若对于任意 ,都有 成立,则 的范围是( )A、 B、
B、 C、(-∞,1)
D、
C、(-∞,1)
D、
二、填空题
-
13. 不等式 的解集是.14. 已知全集U={0,1,2,3,4,5}, , , , ,则用列举法表示集合A=.15. 已知函数 ( 且 )恒过定点 ,则 .16. 数学老师给出一个函数 ,甲、乙、丙、丁四个同学各说出了这个函数的一条性质
甲:在 上函数单调递减;
乙:在 上函数单调递增;
丙:在定义域R上函数的图象关于直线x=1对称;
丁: 不是函数的最小值.
老师说:你们四个同学中恰好有三个人说的正确. 那么,你认为说的是错误.
三、解答题
-
17. 计算下列各式的值:
(Ⅰ)
(Ⅱ) .
18. 设全集 ,集合 ,(Ⅰ)求 ;
(Ⅱ)若集合 ,且 ,求 的取值范围.
19. 设命题p:实数x满足x2-4ax+3a2<0,其中a>0;命题q:实数x满足x2-5x+6≤0.(Ⅰ)若a=1,且p、q均为真命题,求实数x的取值范围;
(Ⅱ)若 是 成立的必要不充分条件,求实数a的取值范围.
20. 如图所示,定义域为 上的函数 是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题. (1)、求 的解析式;(2)、若 关于的方程 有三个不同解,求 的取值范围;(3)、若 ,求 的取值集合.21. 国际上钻石的重量计量单位为克拉.已知某种钻石的价值(美元)与其重量(克拉)的平方成正比,且一颗重为3克拉的该钻石的价值为54 000美元.(1)、写出钻石的价值y关于钻石重量x的函数关系式;(2)、把一颗钻石切割成两颗钻石,若两颗钻石的重量分别为m克拉和n克拉,试求:当 为何值时,价值损失的百分率最大. (注:价值损失的百分率= ;在切割过程中的重量损耗忽略不计)22. 已知:函数 对一切实数 都有 成立,且 .(1)、求 的值;(2)、求 的解析式;(3)、已知 ,设 当 时,不等式 恒成立; 当 时, 是单调函数.如果满足 成立的 的集合记为 ,满足 成立的 的集合记为 ,求 为全集).
(1)、求 的解析式;(2)、若 关于的方程 有三个不同解,求 的取值范围;(3)、若 ,求 的取值集合.21. 国际上钻石的重量计量单位为克拉.已知某种钻石的价值(美元)与其重量(克拉)的平方成正比,且一颗重为3克拉的该钻石的价值为54 000美元.(1)、写出钻石的价值y关于钻石重量x的函数关系式;(2)、把一颗钻石切割成两颗钻石,若两颗钻石的重量分别为m克拉和n克拉,试求:当 为何值时,价值损失的百分率最大. (注:价值损失的百分率= ;在切割过程中的重量损耗忽略不计)22. 已知:函数 对一切实数 都有 成立,且 .(1)、求 的值;(2)、求 的解析式;(3)、已知 ,设 当 时,不等式 恒成立; 当 时, 是单调函数.如果满足 成立的 的集合记为 ,满足 成立的 的集合记为 ,求 为全集).