浙江省绍兴市越城区2017-2018学年七年级上学期数学期末考试试卷
试卷更新日期：2018-12-19 类型：期末考试
一、单选题
-
1. ﹣2018的绝对值是（ ）A、±2018 B、﹣2018 C、 ﹣
D、2018
2. 十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值从54万亿元增长80万亿元，稳居世界第二，其中80万亿用科学记数法表示为（ ）A、8×1012 B、8×1013 C、8×1014 D、0.8×10133. 下列各对数中，互为相反数的是（ ）A、﹣23与﹣32 B、（﹣2）3与﹣23 C、（﹣3）2与﹣32 D、 ﹣
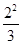与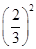 
4. 在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（ ）
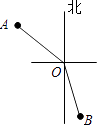A、69° B、111° C、141° D、159°5. 下列说法中正确的是（ ）A、﹣|a|一定是负数 B、近似数2.400万精确到千分位 C、0.5与﹣2互为相反数 D、立方根是它本身的数是0和±16. 下列说法正确的是（ ）A、射线PA和射线AP是同一条射线 B、射线OA的长度是12cm C、直线AB、CD相交于点M D、两点确定一条直线7. 已知一个三角形的周长是3m－n，其中两边长的和为m＋n－4，则这个三角形的第三边的长为（ ）A、2m－4 B、2m－2n－4 C、2m－2n＋4 D、4m－2n＋48. 一把直尺和一块三角板ABC（含30°、60°角）摆放位置如图所示，直尺一边与三角板的两直角边分别交于点D，点E，另一边与三角板的两直角边分别交于点F，点A，且∠CDE=40°，那么∠BAF的大小为（ ）
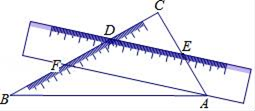A、40° B、45° C、50° D、10°9.填在下面各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（ ）
A、38 B、52 C、66 D、7410. 扑克牌游戏中，小明背对小亮，让小亮按下列四个步骤操作：
①第一步：分发左、中、右三堆牌，每堆牌不少于三张，且各堆牌的张数相同;
②第二步：从左边一堆拿出三张，放入中间一堆;
③第三步：从右边一堆拿出两张，放入中间一堆;
④第四步：左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆.
这时，小明准确说出了中间一堆牌现有的张数，你认为中间一堆的张数是（ ）A、3 B、5 C、7 D、8二、填空题
-
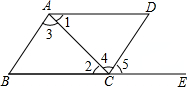
11. 若﹣7xm+2y与﹣3x3yn是同类项，则m= ， n= ．12. 的算术平方根是13. 如图，下列条件中：
①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5；
则一定能判定AB∥CD的条件有(填写所有正确的序号)．
14. 若x﹣3y=﹣4，则代数式5+6y﹣2x的值是 ．15. 规定：用{m}表示大于m的最小整数，例如{ }=3，{5}=6，{﹣1.3}=﹣1等；用[m]表示不大于m的最大整数，例如[ ]=3，[4]=4，[﹣1.5]=﹣2，如果整数x满足关系式：2{x}+3[x]=12，则x= ．三、解答题
-
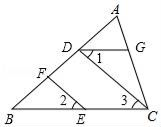
16. 计算：(1)、|﹣4|×7﹣（﹣8）；(2)、﹣14﹣2× ．17. 先化简，再求值：（a2b﹣ab）﹣2（ab2﹣ba），其中（2a+1）2+|b﹣2|=0．18. 解方程：(1)、6+2（x﹣3）=x；(2)、1﹣ ．19. 如图，EF∥CD，∠1=∠2，求证：DG∥BC．
20. 为了提升绍兴城市环境品质，以杭州G20环境提升为标准，我市最近进行景观环境改造提升，学校也积极响应，组织学生植树活动，已知在甲处植树的有23人，在乙处植树的有17人，现调20人取支援，使在甲处植树的人数是乙处植树人数的2倍多3人，应调往甲、乙两处各多少人？21. 如图，直线AB、CD相交于点O，∠BOM=90°，∠DON=90°．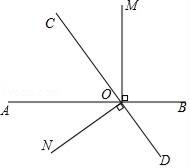
(1)、若∠COM=∠AOC，求∠AOD的度数；(2)、若∠COM= ∠BOC，求∠AOC和∠MOD．22. 如图1，有A、B两动点在线段MN上各自做不间断往返匀速运动（即只要动点与线段MN的某一端点重合则立即转身以同样的速度向MN的另一端点运动，与端点重合之前动点运动方向、速度均不改变），已知A的速度为3米/秒，B的速度为2米/秒
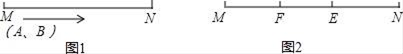(1)、已知MN=100米，若B先从点M出发，当MB=5米时A从点M出发，A出发后经过秒与B第一次重合；(2)、已知MN=100米，若A、B同时从点M出发，经过秒A与B第一次重合；(3)、如图2，若A、B同时从点M出发，A与B第一次重合于点E，第二次重合于点F，且EF=20米，设MN=s米，列方程求s．