广西合浦县2018届九年级上学期数学期末考试试卷
试卷更新日期：2018-12-19 类型：期末考试
一、单选题
-
1. Rt△ABC中，∠C=90°，a=4，b=3，则cosA的值是（ ）A、
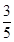B、
C、
D、
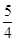2. 有四张背面一模一样的卡片，卡片正面分别写着一个函数关系式，分别是 ，将卡片顺序打乱后，随意从中抽取一张，取出的卡片上的函数是 随 的增大而增大的概率是（ ）A、 B、 C、 D、13. 某几何体的三视图如图，则该几何体是（ ）
A、圆柱 B、圆锥 C、球 D、长方体4.如图所示几何体的左视图是（ ）
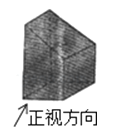A、
B、
C、
D、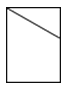
5. 下面是一天中四个不同时刻两座建筑物的影子，将它们按时间先后顺序正确的是（ ）
A、③①④② B、③②①④ C、③④①② D、②④①③6. 四个数－2，0， ，π，其中是无理数的是（ ）A、－2 B、0 C、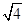
D、π
7. 一个不透明的布袋里装有6个黑球和3个白球，它们除颜色外其余都相同，从中任意摸出一个球，是白球的概率为（ ）A、 B、
C、
D、
8. 如图，下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么涂黄色、白色、红色的对面分别是（ ）
A、蓝色、绿色、黑色 B、绿色、蓝色、黑色 C、绿色、黑色、蓝色 D、蓝色、黑色、绿色9. 如图，点I和O分别是△ABC的内心和外心，则∠AIB和∠AOB的关系为（ ）
A、∠AIB=∠AOB B、∠AIB≠∠AOB C、4∠AIB-∠AOB=360° D、2∠AOB-∠AIB=180°10. 甲、乙两位同学在一次实验中统计了某一结果出现的频率，给出的统计图如图所示，则 符合这一结果的实验可能是（ ）
A、掷一枚正六面体的骰子，出现6点的概率 B、掷一枚硬币，出现正面朝上的概率 C、任意写出一个整数，能被2整除的概率 D、一个袋子中装着只有颜色不同，其他都相同的两个红球和一个黄球，从中任意取出一个是黄球的概率11. 顶点为（5，1），形状与函数y= x 2 的图象相同且开口方向相反的抛物线是（ ）A、 y=-
(x-5) 2+1
B、 y= x 2- 5
C、 y=- （x-5）2- 1
D、 y= （x+5）2 -1
12. 从长度分别为2、3、4、5的4条线段中任取3条，能构成钝角三角形的概率为（ ）A、 B、 C、
D、
二、填空题
-
13.
如图，矩形ABCD中，AD=3，∠CAB=30°，点P是线段AC上的动点，点Q是线段CD上的动点，则AQ+QP的最小值是 ．
14. 已知点A（1，2）在反比例函数y= 的图象上，则当x＞1时，y的取值范围是 ．15. 已知y=x2+mx-6，当1≤m≤3，y<0恒成立，那么实数x的取值范围是。
16. 已知二次函数y=ax 2 +bx+c中，函数y与自变量x的部分对应值如下表：则当2＜y＜5时，x的取值范围是
三、解答题
-
17. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小李做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
(1)、请估计：当实验次数为5000次时，摸到白球的频率将会接近；（精确到0.1）(2)、假如你摸一次，你摸到白球的概率P（摸到白球）= ；(3)、试验估算这个不透明的盒子里黑球有多少只？18. 有2个信封A、B，信封A装有四张卡片上分别写有1、2、3、4，信封B装有三张卡片分别写有5、6、7，每张卡片除了数字没有任何区别．从这两个信封中随机抽取两张卡片．(1)、请你用列表法或画树状图的方法描述所有可能的结果；(2)、把卡片上的两个数相加，求“得到的和是3的倍数”的概率．19. 指出下列句子的错误，并加以改正：
(1)、如图1，在线段AB的延长线上取一点C；(2)、如图2，延长直线AB，使它与直线CD相交于点P；(3)、如图3，延长射线OA，使它和线段BC相交于点D．20. 知识是用来为人类服务的，我们应该把它们用于有意义的方面．下面就两个情景请你作出评判．情景一：从教室到图书馆，总有少数同学不走人行道而横穿草坪，这是为什么呢？试用所学数学知识来说明这个问题．
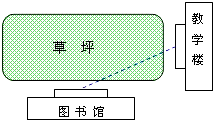
情景二：A、B是河流l两旁的两个村庄，现要在河边修一个抽水站向两村供水，问抽水站修在什么地方才能使所需的管道最短？请在图中表示出抽水站点P的位置，并说明你的理由：
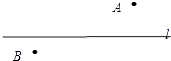
你赞同以上哪种做法？你认为应用数学知识为人类服务时应注意什么？