广西防城港市2018届九年级上学期数学期末考试试卷
试卷更新日期:2018-12-19 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
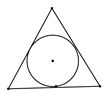 B、
B、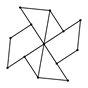 C、
C、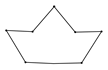 D、
D、 2. 下列方程是一元二次方程的是( )A、x﹣2=0 B、x2﹣4x﹣1=0 C、x3﹣2x﹣3=0 D、xy+1=03. 下列事件中,是必然事件的是( )A、明天太阳从东方升起 B、打开电视机,正在播放体育新闻 C、射击运动员射击一次,命中靶心 D、经过有交通信号灯的路灯,遇到红灯4. 如图,点A,B,C都在⊙O上,若∠C=35°,则∠AOB的度数为( )
2. 下列方程是一元二次方程的是( )A、x﹣2=0 B、x2﹣4x﹣1=0 C、x3﹣2x﹣3=0 D、xy+1=03. 下列事件中,是必然事件的是( )A、明天太阳从东方升起 B、打开电视机,正在播放体育新闻 C、射击运动员射击一次,命中靶心 D、经过有交通信号灯的路灯,遇到红灯4. 如图,点A,B,C都在⊙O上,若∠C=35°,则∠AOB的度数为( )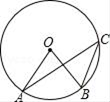 A、35° B、55° C、145° D、70°5. 抛物线y=2(x﹣1)2+3的对称轴为( )A、直线x=1 B、直线y=1 C、直线y=﹣1 D、直线x=﹣16. 在平面直角坐标系中,点P(1,2)关于原点对称的点的坐标是( )A、(﹣1,﹣2) B、(﹣1,2) C、(1,﹣2) D、(2,1)7. 下列说法正确的是( )A、三点确定一个圆 B、三角形的外心到三角形各顶点的距离相等 C、相等的圆心角所对的弧相等 D、圆内接四边形的对角互余8. 已知袋中有若干个球,其中只有2个红球,它们除颜色外其它都相同.若随机从中摸出一个,摸到红球的概率是 ,则袋中球的总个数是( )A、2 B、4 C、6 D、89. 在⊙O中,已知半径为5,弦AB的长为8,则圆心O到AB的距离为( )A、3 B、4 C、5 D、610. 关于x的方程x2﹣2x+m=0有两个相等的实数根,则实数m的取值范围为( )A、m≥1 B、m<1 C、m=1 D、m<﹣111. 如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D,若PA=5,则△PCD的周长为( )
A、35° B、55° C、145° D、70°5. 抛物线y=2(x﹣1)2+3的对称轴为( )A、直线x=1 B、直线y=1 C、直线y=﹣1 D、直线x=﹣16. 在平面直角坐标系中,点P(1,2)关于原点对称的点的坐标是( )A、(﹣1,﹣2) B、(﹣1,2) C、(1,﹣2) D、(2,1)7. 下列说法正确的是( )A、三点确定一个圆 B、三角形的外心到三角形各顶点的距离相等 C、相等的圆心角所对的弧相等 D、圆内接四边形的对角互余8. 已知袋中有若干个球,其中只有2个红球,它们除颜色外其它都相同.若随机从中摸出一个,摸到红球的概率是 ,则袋中球的总个数是( )A、2 B、4 C、6 D、89. 在⊙O中,已知半径为5,弦AB的长为8,则圆心O到AB的距离为( )A、3 B、4 C、5 D、610. 关于x的方程x2﹣2x+m=0有两个相等的实数根,则实数m的取值范围为( )A、m≥1 B、m<1 C、m=1 D、m<﹣111. 如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D,若PA=5,则△PCD的周长为( ) A、5 B、7 C、8 D、1012. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①ac<0;②方程ax2+bx+c=0的两根是x1=﹣1,x2=3;③b=2a;④函数的最大值是c﹣a.其中正确的是( )
A、5 B、7 C、8 D、1012. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列四个结论:①ac<0;②方程ax2+bx+c=0的两根是x1=﹣1,x2=3;③b=2a;④函数的最大值是c﹣a.其中正确的是( ) A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
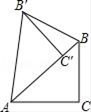
13. 抛物线y=x2+5x﹣1的开口方向是 .14. 掷一个质地均匀的正方体骰子,向上一面的点数为奇数的概率是 .15. 将抛物线y=-x2向左平移2个单位后,得到的抛物线的解析式是 .16. 如图,把Rt△ABC绕点A逆时针旋转44°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠B′BC′= .
 17. 某工程一月份的产值为600万元,三月份的产值达到了726万元,设每月产值的增长率x相同,则可列出方程为 .
17. 某工程一月份的产值为600万元,三月份的产值达到了726万元,设每月产值的增长率x相同,则可列出方程为 .三、解答题
-
18. 解关于x的方程:x2﹣4x=0.19. 如图,在⊙O中,弦AB与DC相交于E,且BE=DE,求证: .
 20. 已知2是关于x的方程x2﹣2mx+3m=0的一个根,而这个方程的两个根恰好是等腰△ABC的两条边长.(1)、求m的值;(2)、求△ABC的周长.21. 如图,在方格纸上,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′、B′、C′).
20. 已知2是关于x的方程x2﹣2mx+3m=0的一个根,而这个方程的两个根恰好是等腰△ABC的两条边长.(1)、求m的值;(2)、求△ABC的周长.21. 如图,在方格纸上,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′、B′、C′). (1)、画出旋转后的△A′B′C′;(2)、求点A在旋转过程中所经过的路线的长.(结果保留π)22. 如图,均匀的正四面体的各面依次标有1,2,3,4四个数字,小明做了60次投掷试验,结果统计如下:
(1)、画出旋转后的△A′B′C′;(2)、求点A在旋转过程中所经过的路线的长.(结果保留π)22. 如图,均匀的正四面体的各面依次标有1,2,3,4四个数字,小明做了60次投掷试验,结果统计如下:朝下数字
1
2
3
4
出现的次数
16
20
14
10
 (1)、求上述试验中“2朝下”的频率;(2)、随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于5的概率.23. 某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.(1)、用含x的代数式表示:每件商品的销售价为元,每件商品的利润为元,每周的商品销售量为件;(2)、求y关于x的函数关系式(不要求写出x的取值范围);(3)、应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?
(1)、求上述试验中“2朝下”的频率;(2)、随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于5的概率.23. 某商品的进货价为每件30元,为了合理定价,先投放市场试销.据市场调查,销售价为每件40元时,每周的销售量是180件,而销售价每上涨1元,则每周的销售量就会减少5件,设每件商品的销售价上涨x元,每周的销售利润为y元.(1)、用含x的代数式表示:每件商品的销售价为元,每件商品的利润为元,每周的商品销售量为件;(2)、求y关于x的函数关系式(不要求写出x的取值范围);(3)、应怎样确定销售价,使该商品的每周销售利润最大?最大利润是多少?

