浙江省绍兴市2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2018-12-19 类型:期末考试
一、单选题
-
1. 下列交通标志图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 不等式x+3<5的解集在数轴上表示为( )A、
2. 不等式x+3<5的解集在数轴上表示为( )A、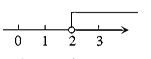 B、
B、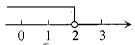 C、
C、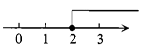 D、
D、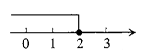 3. 能说明命题“对于任何实数a,|a|>﹣a”是假命题的一个反例可以是( )A、a=﹣2 B、 a=
3. 能说明命题“对于任何实数a,|a|>﹣a”是假命题的一个反例可以是( )A、a=﹣2 B、 a= C、a=1
D、 a=
C、a=1
D、 a= 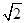 4. 过点Q(0,4)的一次函数的图象与正比例函数 的图象相交于点P(1,2),则这个一次函数图象的解析式是( ).
4. 过点Q(0,4)的一次函数的图象与正比例函数 的图象相交于点P(1,2),则这个一次函数图象的解析式是( ).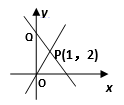 A、
A、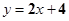 B、
B、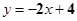 C、
C、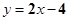 D、
D、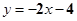 5. 以下命题的逆命题为真命题的是( )A、对顶角相等 B、同旁内角互补,两直线平行 C、若a=b,则a2=b2 D、若a>0,b>0,则a2+b2>06. 点M(﹣5,y)向下平移5个单位所得的像是关于x轴对称,则y的值是( )A、﹣5 B、5 C、
5. 以下命题的逆命题为真命题的是( )A、对顶角相等 B、同旁内角互补,两直线平行 C、若a=b,则a2=b2 D、若a>0,b>0,则a2+b2>06. 点M(﹣5,y)向下平移5个单位所得的像是关于x轴对称,则y的值是( )A、﹣5 B、5 C、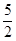 D、
D、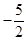 7. 如图,将△ABC沿DE,HG,EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )
7. 如图,将△ABC沿DE,HG,EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )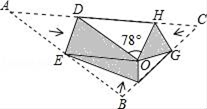 A、78° B、102° C、120° D、112°8. 化简: =( )A、2x﹣6 B、0 C、6﹣2x D、2x+69. 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD= ,则BC的长为( )
A、78° B、102° C、120° D、112°8. 化简: =( )A、2x﹣6 B、0 C、6﹣2x D、2x+69. 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD= ,则BC的长为( )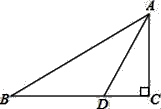 A、 ﹣1 B、 +1 C、 ﹣1 D、 +110. 如图,直线y=x+2与y轴相交于点A0 , 过点A0作 轴的平行线交直线y=0.5x+1于点B1 , 过点 B1作 轴的平行线交直线y=x+2于点A1 , 再过点 作 轴的平行线交直线y=0.5x+1于点B2 , 过点 B2作 轴的平行线交直线y=x+2于点A2 , …,依此类推,得到直线y=x+2上的点A1 ,A2 ,A3 ,…,与直线y=0.5x+1上的点B1 , B2 , B3 , …,则A7B8的长为( )
A、 ﹣1 B、 +1 C、 ﹣1 D、 +110. 如图,直线y=x+2与y轴相交于点A0 , 过点A0作 轴的平行线交直线y=0.5x+1于点B1 , 过点 B1作 轴的平行线交直线y=x+2于点A1 , 再过点 作 轴的平行线交直线y=0.5x+1于点B2 , 过点 B2作 轴的平行线交直线y=x+2于点A2 , …,依此类推,得到直线y=x+2上的点A1 ,A2 ,A3 ,…,与直线y=0.5x+1上的点B1 , B2 , B3 , …,则A7B8的长为( ) A、64 B、128 C、256 D、512
A、64 B、128 C、256 D、512二、填空题
-
11. 函数 的自变量x的取值范围是 .12. 12.若二次根式 是最简二次根式,则最小的正整数 =13. 一次函数y=(k﹣3)x﹣k+2的图象经过第一、三、四象限.则k的取值范围是 .14. 若线段AB平行于x轴,AB长为5,若A的坐标为(4,5),则B的坐标为 .15. 已知函数y1=k1x+b1与函数y2=k2x+b2的图象如图所示,则不等式k1x+b1<k2x+b2的解集是 .
 16. 如图,平面直角坐标系中有一正方形OABC,点C的坐标为(﹣2,﹣1),则点A坐标为 , 点B坐标为 .
16. 如图,平面直角坐标系中有一正方形OABC,点C的坐标为(﹣2,﹣1),则点A坐标为 , 点B坐标为 .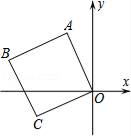 17.
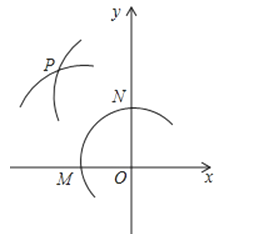
17.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(2a,b+1),则a与b的数量关系为 .
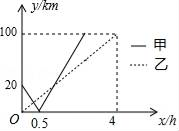
 18. 沿河岸有A,B,C三个港口,甲乙两船同时分别从AB港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
18. 沿河岸有A,B,C三个港口,甲乙两船同时分别从AB港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:①乙船的速度是25km/h;②从A港到C港全程为120km;③甲船比乙船早1.5小时到达终点;④若设图中两者相遇的交点为P点,P点的坐标为( , );⑤如果两船相距小于10km能够相互望见,那么甲、乙两船可以相互望见时,x的取值范围是 <x<2.其中正确的结论有 .
三、解答
-
19. 计算:20. 解不等式组 ,并将其解集表示在数轴上.
 21. 方格纸中小正方形的顶点叫格点.点A和点B是格点,位置如图.
21. 方格纸中小正方形的顶点叫格点.点A和点B是格点,位置如图.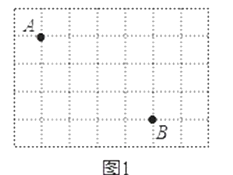 (1)、在图1中确定格点C使△ABC为直角三角形,画出一个这样的△ABC;
(1)、在图1中确定格点C使△ABC为直角三角形,画出一个这样的△ABC;
(2)、在图2中确定格点D使△ABD为等腰三角形,画出一个这样的△ABD; (3)、在图2中满足题(2)条件的格点D有个.
(3)、在图2中满足题(2)条件的格点D有个.
22. 如图,△AOB,△COD是等腰直角三角形,点D在AB上,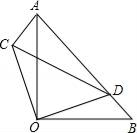 (1)、求证:△AOC≌△BOD;(2)、若AD=3,BD=1,求CD.23. 某商店销售A型和B型两种型号的电脑,销售一台A型电脑可获利120元,销售一台B型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的3倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.(1)、求y与x的关系式;(2)、该商店购进A型、B型电脑各多少台,才能使销售利润最大?(3)、若限定商店最多购进A型电脑60台,则这100台电脑的销售总利润能否为13600元?若能,请求出此时该商店购进A型电脑的台数;若不能,请求出这100台电脑销售总利润的范围.24. 如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2= x+b过点P.
(1)、求证:△AOC≌△BOD;(2)、若AD=3,BD=1,求CD.23. 某商店销售A型和B型两种型号的电脑,销售一台A型电脑可获利120元,销售一台B型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的3倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.(1)、求y与x的关系式;(2)、该商店购进A型、B型电脑各多少台,才能使销售利润最大?(3)、若限定商店最多购进A型电脑60台,则这100台电脑的销售总利润能否为13600元?若能,请求出此时该商店购进A型电脑的台数;若不能,请求出这100台电脑销售总利润的范围.24. 如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2= x+b过点P.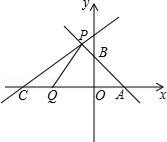 (1)、求点P坐标和b的值;(2)、若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.
(1)、求点P坐标和b的值;(2)、若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;
②求出t为多少时,△APQ的面积小于3;
③是否存在t的值,使△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.