浙江省江北区2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期：2018-12-19 类型：期末考试
一、单选题
-
1. 1．平面直角坐标系中A（2，-3）所在的象限为（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 不等式2x＞﹣3的解是（ ）A、 x＜
B、 x＞﹣
C、 x＜﹣ 
D、 x＞﹣
3. 以下图形中对称轴条数最多的是 （ ）A、
B、
C、
D、
4. 函数y= 中，自变量x的取值范围是（ ）A、x＞﹣2 B、x≠0 C、x＞﹣2且x≠0 D、x≠﹣25. 如图，在△ABC中，∠A=35°，∠C=45°，则与∠ABC相邻的外角的度数是（ ）
A、35° B、45° C、80° D、100°6. 如图所示，在△ABC中，AB=AC，D、E分别是AC、AB的中点，且BD，CE相交于O点，某一位同学分析这个图形后得出以下结论： ①△BCD≌△CBE； ②△BDA≌△CEA； ③△BOE≌△COD； ④△BAD≌△BCD；⑤△ACE≌△BCE，上述结论一定正确的是（ ）
A、①②③ B、②③④ C、①③⑤ D、①③④7. 下列各组数中，不能作为直角三角形三边长的是（ ）A、1.5，2，3 B、5，12，13 C、7，24，25 D、8，15，178. 已知等腰三角形的其中两边长分别为4，9，则这个等腰三角形的周长是（ ）A、13 B、17 C、22 D、17或229. 在平面直角坐标系中，若有一点P（2，1）向上平移3个单位或向左平移4个单位，恰好都在直线y=kx+b上，则k的值是（ ）A、
B、
C、
D、2
10. 如图，点D是正△ABC内的一点，DB=3，DC=4，DA=5，则∠BDC的度数是（ ）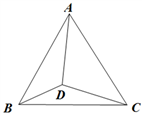
A、120° B、135° C、140° D、150°二、填空题
-
11. 小明的身高h超过了160cm，用不等式可表示为.12. 命题“若a,b互为倒数，则ab=1”的逆命题是.13. 已知△ABC≌△DEF，若AB=5，BC=6，AC=8，则△DEF的周长是.14. 在第二象限到x轴距离为2，到y轴距离为5的点的坐标是.15. 在Rt△中有一个内角为30°，且斜边和较短直角边之和为15cm，则这个直角三角形的斜边长上的中线长为cm.16. 已知等腰三角形的腰长为xcm，顶角平分线与对边的交点到一腰的距离为4cm，这个等腰三角形的面积为ycm2 ， 则y与x的函数关系式为.17. 如图，在Rt△ABC中，∠C=90°，斜边AB的垂直平分线交AB于点E，交BC于点D，若∠B=35°，则∠CAD=°.
18. 一次函数y=kx+b的图象经过A(-1，1）和B(- ，0），则不等式组 的解为.
三、解答题
-
19. 解不等式组 并把它的解表示在数轴上.20. 请你用直尺和圆规作图（要求：不必写作法，但要保留作图痕迹）.已知：∠AOB，点M、N．求作：点P，使点P到OA、OB的距离相等，且PM=PN．
21. 如图，C是线段AB的中点，CD∥BE，且CD=BE，求证：AD=CE．
22. 如图，△ABC在平面直角坐标系内.
(1)、试写出△ABC各顶点的坐标；(2)、求出△ABC的面积．23. 宁波某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共10台，具体情况如下表：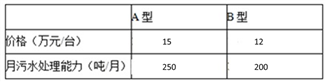
经预算，企业最多支出136万元购买设备，且要求月处理污水能力不低于2150吨．
(1)、该企业有哪几种购买方案？(2)、哪种方案更省钱？并说明理由．24. 甲、乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走. 设甲、乙两人相距 （米），甲行走的时间为 （分）， 关于 的函数图象的一部分如图所示.
(1)、求甲行走的速度；(2)、在坐标系中，补画 关于 函数图象的其余部分，并写出已画图象另一个端点的坐标；(3)、问甲、乙两人何时相距390米？25. 如图，已知∠ABC=90°，△ABE是等边三角形，点P为射线BC上任意一点（点P与点B不重合），连接AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连接QE并延长交射线BC于点F．
(1)、如图，当BP=BA时，∠EBF=°，猜想∠QFC =°；(2)、如图，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明．(3)、已知线段AB＝ ，设BP＝x，点Q到射线BC的距离为y，求y关于x的函数关系式．