浙江省杭州市西湖区2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2018-12-19 类型:期末考试
一、单选题
-
1. 点P(1,3)向下平移2个单位后的坐标是( )A、(1,2) B、(0,1) C、(1,5) D、(1,1)2. 不等式x﹣1>0 的解在数轴上表示为( )
A、 B、
B、 C、
C、 D、
D、 3. 以a,b,c为边的三角形是直角三角形的是( )A、a=2,b=3,c=4 B、 a=1,b= ,c=2 C、a=4,b=5,c=6 D、 a=2,b=2,c=
3. 以a,b,c为边的三角形是直角三角形的是( )A、a=2,b=3,c=4 B、 a=1,b= ,c=2 C、a=4,b=5,c=6 D、 a=2,b=2,c=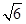 4. 对于命题“若a2=b2”,则“a=b”下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=3 B、a=﹣3,b=﹣3 C、a=3,b=﹣3 D、a=﹣3,b=﹣25. 若x+a<y+a,ax>ay,则( )
4. 对于命题“若a2=b2”,则“a=b”下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=3 B、a=﹣3,b=﹣3 C、a=3,b=﹣3 D、a=﹣3,b=﹣25. 若x+a<y+a,ax>ay,则( )
A、x>y,a>0 B、x>y,a<0 C、x<y,a>0 D、x<y,a<06. 已知y=kx+k的图象与y=x的图象平行,则y=kx+k的大致图象为( )A、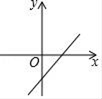 B、
B、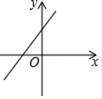 C、
C、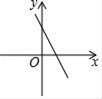 D、
D、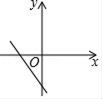 7. 如图,若△ABC的周长为20,则AB的长可能为( )
7. 如图,若△ABC的周长为20,则AB的长可能为( )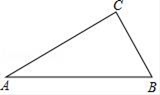 A、8 B、10 C、12 D、148. 如图,△ABC中,D为AB的中点,BE⊥AC,垂足为E.若DE=4,AE=6,则BE的长度是( )
A、8 B、10 C、12 D、148. 如图,△ABC中,D为AB的中点,BE⊥AC,垂足为E.若DE=4,AE=6,则BE的长度是( )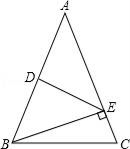 A、10 B、 2 C、8 D、 2
A、10 B、 2 C、8 D、 2 9. 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,将△ABC绕点B顺时针旋转60°,得到△BDE,连结DC交AB于点F,则△ACF与△BDF的周长之和为( )
9. 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,将△ABC绕点B顺时针旋转60°,得到△BDE,连结DC交AB于点F,则△ACF与△BDF的周长之和为( )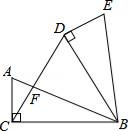 A、44 B、43 C、42 D、4110. 关于函数y=(k﹣3)x+k,给出下列结论:
A、44 B、43 C、42 D、4110. 关于函数y=(k﹣3)x+k,给出下列结论:①此函数是一次函数,②无论k取什么值,函数图象必经过点(﹣1,3),③若图象经过二、三、四象限,则k的取值范围是k<0,④若函数图象与x轴的交点始终在正半轴可得k<3.其中正确的是( )
A、①② B、①③ C、②③ D、③④二、填空题
-
11. 若函数y=2x+b(b为常数)的图象经过点A(0,﹣2),则b= .12. 若不等式组 的解集是-1<x<2,则 .13. 已知一个等腰三角形两内角的度数之比为1∶4,则这个等腰三角形顶角的度数为 .14. 一次数学知识竞赛中,竞赛题共30题.规定:答对一道题得4分,不答或答错一道题倒扣2分,甲同学答对25道题,答错5道题,则甲同学得分;若得分不低于60分者获奖,则获奖者至少应答对道题.15. 关于函数y=﹣2x+1,下列说法:
①图象必经过点(1,0),②直线y=2x﹣1与y=﹣2x+1相交,③当x> 时,y<0,④y随x增大而减小.其中正确的序号是 .
16. 如图,点A的坐标为(4,0),点B从原点出发,沿y轴负方向以每秒1个单位长度的速度运动,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF,等腰Rt△ABE,连结EF交y轴于P点,当点B在y轴上运动时,经过t秒时,点E的坐标是(用含t的代数式表示),PB的长是 .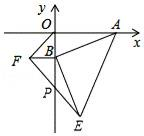
三、解答题
-
17. 已知点P(a+1,2a﹣1)在第四象限,求a的取值范围.18. 在平面直角坐标系中,点A(1,1),B(4,3),将点A向左平移2个单位长度,再向上平移3个单位长度得到点C.
 (1)、写出点C的坐标;(2)、画出△ABC并判断△ABC的形状.19. 如图,在△ABC中,AB=AC,∠1=∠2,则△ABD与△ACD全等吗?证明你的判断.
(1)、写出点C的坐标;(2)、画出△ABC并判断△ABC的形状.19. 如图,在△ABC中,AB=AC,∠1=∠2,则△ABD与△ACD全等吗?证明你的判断.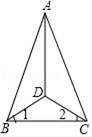 20. 对于任意实数a,b,定义关于@的一种运算如下:a@b=2a﹣b,例如:5@3=10﹣3=7,(﹣3)@5=﹣6﹣5=﹣11.(1)、若x@3<5,求x的取值范围;(2)、已知关于x的方程2(2x﹣1)=x+1的解满足x@a<5,求a的取值范围.21. 如图,在平面直角坐标系中,长方形OABC的边OC=2,将过点B的直线y=x﹣3与x轴交于点E.
20. 对于任意实数a,b,定义关于@的一种运算如下:a@b=2a﹣b,例如:5@3=10﹣3=7,(﹣3)@5=﹣6﹣5=﹣11.(1)、若x@3<5,求x的取值范围;(2)、已知关于x的方程2(2x﹣1)=x+1的解满足x@a<5,求a的取值范围.21. 如图,在平面直角坐标系中,长方形OABC的边OC=2,将过点B的直线y=x﹣3与x轴交于点E. (1)、求点B的坐标;(2)、连结CE,求线段CE的长;(3)、若点P在线段CB上且OP= ,求P点坐标.22. 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)、求点B的坐标;(2)、连结CE,求线段CE的长;(3)、若点P在线段CB上且OP= ,求P点坐标.22. 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.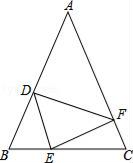 (1)、求证:△DEF是等腰三角形;(2)、当∠A=50°时,求∠DEF的度数;(3)、若∠A=∠DEF,判断△DEF是否为等腰直角三角形.23. 一次函数y=kx+b的图象经过点A(0,9),并且与直线y= x相交于点B,与x轴相交于点C.
(1)、求证:△DEF是等腰三角形;(2)、当∠A=50°时,求∠DEF的度数;(3)、若∠A=∠DEF,判断△DEF是否为等腰直角三角形.23. 一次函数y=kx+b的图象经过点A(0,9),并且与直线y= x相交于点B,与x轴相交于点C.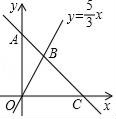 (1)、若点B的横坐标为3,求B点的坐标和k,b的值;(2)、在y轴上是否存在这样的点P,使得以点P,B,A为顶点的三角形是等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由.(3)、在直线y=kx+b上是否存在点Q,使△OBQ的面积等于 ?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)、若点B的横坐标为3,求B点的坐标和k,b的值;(2)、在y轴上是否存在这样的点P,使得以点P,B,A为顶点的三角形是等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由.(3)、在直线y=kx+b上是否存在点Q,使△OBQ的面积等于 ?若存在,请求出点Q的坐标;若不存在,请说明理由.