浙江省海曙区2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2018-12-19 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,下列各点在第一象限的是( )A、(1,2) B、(1,-2) C、(-1,-2) D、(-1,2)
-
2. 下列语句是命题的是( )A、延长线段AB B、过点A作直线a的垂线 C、对顶角相等 D、x与y相等吗?
-
3. 下列不等式对任何实数x都成立的是( )A、x+1>0 B、x2+1>0 C、x2+1<0 D、∣x∣+1<0
-
4. 若一个三角形三边a,b,c满足(a+b)2=c2+2ab,则这个三角形是( )A、等边三角形 B、钝角三角形 C、等腰直角三角形 D、直角三角形
-
5. 平面直角坐标系内有点A(-2,3), B(4,3), 则A,B相距( )A、4个单位长度 B、5个单位长度 C、6个单位长度 D、10个单位长度
-
6. 下列条件中不能判定三角形全等的是( )A、两角和其中一角的对边对应相等 B、三条边对应相等 C、两边和它们的夹角对应相等 D、三个角对应相等
-
7. 不等式-2x+6>0的正整数解有( )A、无数个 B、0个 C、1个 D、2个
-
8. 如图,△ABC中,AB=AC.将△ABC沿AC方向平移到△DEF位置,点D在AC上,连结BF.若AD=4,BF=8,∠ABF=90°,则AB的长是( )
 A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8 -
9. 平面直角坐标系中,将直线l向右平移1个单位长度得到的直线解析式是y=2x+2,则原来的直线解析式是( )A、y=3x+2 B、y=2x+4 C、y=2x+1 D、y=2x+3
-
10. 如图,△ABC中,∠A=67.5°,BC=4,BE⊥CA于E,CF⊥AB于 F,D是BC的中点.以F为原点,FD所在直线为x轴构造平面直角坐标系,则点E的横坐标是( )
 A、 2-
A、 2-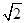 B、
B、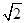 -1
C、 2-
D、
-1
C、 2-
D、
二、填空题
-
11. 函数y= 的自变量x的取值范围是 .
-
12. 如图,△ABC中,AB=AC,∠B=70°,则∠A=
-
13. 点A(2,3)关于x轴的对称点是。
-
14. 若4,5,x是一个三角形的三边,则x的值可能是 (填写一个即可)
-
15. 如图,△ABC中,∠C=90°,点D是BC上一点,连结AD.若CD=3, ∠B=40°,∠CAD=25°,则点D到AB的距离为

-
16. 若不等式组 的解集是x<4,则m的取值范围是

-
17. 如图,直线y=-2x+2与x轴交于A点,与y轴交于B点.过点B作直线BP与x轴交于P点,若△ABP的面积是3,则P点的坐标是

-
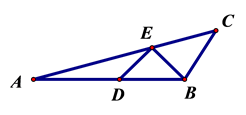
18. 如图,△ABC中, ∠A=15°,AB是定长.点D,E分别在AB,AC上运动, 连结BE,ED.若BE+ED的最小值是2, 则AB的长是
三、解答题
-
19. 解下列不等式(组),并把解集在数轴上表示出来.(1)、
 (2)、
(2)、
-
20. 平面直角坐标系中, △ABC的三个顶点坐标分别为A(3,4), B(2,0), C(-1,2).

①在图中画出△ABC;
②将△ABC向下平移4个单位得到△DEF(点A,B,C分别对应点D,E,F),在图中画出△DEF,并求EF的长.
-
21. 如图,已知在△ABC与△ADC中, AB=AD.
 (1)、若∠B=∠D=90°,求证: △ABC≌△ADC;(2)、若∠B=∠D≠90°,求证:BC=DC.
(1)、若∠B=∠D=90°,求证: △ABC≌△ADC;(2)、若∠B=∠D≠90°,求证:BC=DC. -
22. 随着人民生活水平的提高,越来越多的家庭采取分户式采暖,降低采暖用气价格的呼声强烈.某市物价局对市区居民管道天然气阶梯价格制度的规定作出了调整,调整后的付款金额y(单位:元)与年用气量(单位:m3)之间的函数关系如图所示:
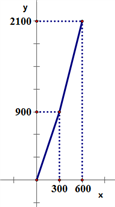 (1)、宸宸家年用气量是270m3 , 求付款金额.(2)、皓皓家去年的付款金额是1300元,求去年的用气量.
(1)、宸宸家年用气量是270m3 , 求付款金额.(2)、皓皓家去年的付款金额是1300元,求去年的用气量. -
23. 自2009年起,每年的11月11日是Tmall一年一度全场大促销的日子.某服饰店对某商品推出促销活动:双十一当天,买两件等值的商品可在每件原价减50元的基础上,再打八折;如果单买,则按原价购买.(1)、妮妮看中两件原价都是300元的此类商品, 则在双十一当天,购买这两件商品总共需要多少钱?(2)、熊熊购买了两件等值的此类商品后, 发现比两件一起按原价六折购买便宜. 若这两件等值商品的价格都是大于196的整数, 则原价可能是多少元?
-
24. △ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.

 (1)、如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)(2)、如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.(3)、如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点.
(1)、如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)(2)、如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.(3)、如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点.①若BD= ,求四边形BCDE的面积;
②若AB=3,AD=2,设CD2=x,EB2=y,求y与x之间的函数关系式.
