广西岳池县2017-2018学年八年级上学期数学期末考试试卷

试卷更新日期：2018-12-19 类型：期末考试

进入出卷网下载

一、单选题

1. 点A（3，4）关于x轴对称的点的坐标为（）

A、（－3，4） B、（4，3） C、（－3，－4） D、（3，－4）

查看试题解析
2. 一个三角形的三边长分别为x、2、3，那么x的取值范围是：（）

A、1＜x＜5 B、2＜x＜3 C、2＜x＜5 D、x＞2

查看试题解析
3. 下列计算正确的是（）

A、a³+a²=2a⁵ B、a³·a²=a⁶ C、a³÷a²=a D、（a³）²=a⁹

查看试题解析
4. 把分式 $\frac{2 a b}{a + b}$ 中的a，b都扩大到原来的2倍，则分式的值（）

A、扩大到原来的4倍 B、扩大到原来的2倍 C、缩小到原来的 D、不变

查看试题解析
5. 如图，AC、BD相交于点O，∠1=∠2，若用“SAS”说明△ACB≌△BDA，则还需要加上条件（）

A、AD=BC B、BD=AC C、∠D=∠C D、OA=AB

查看试题解析
6. 多边形的每个内角都等于140°，从此多边形的一个顶点出发可作的对角线共有（）

A、6条 B、7条 C、8条 D、9条

查看试题解析
7. 在△ABC中，AB=AC，AB的垂直平分线交AB于点D，交直线AC于点E，∠AEB=70°，那么∠BAC等于（）

A、65° B、55° C、55° 或125° D、65°或115°

查看试题解析
8. 已知a^m=2，aⁿ=3，则a^3m+2n的值是（）

A、24 B、36 C、72 D、6．

查看试题解析
9. 如图，AD∥BC，∠ABC的平分线BP与∠BAD的平分线AP相交于点P，作PE⊥AB于点E.若PE＝3，则两平行线AD与BC间的距离为（）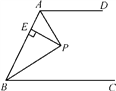

A、3 B、4 C、5 D、6

查看试题解析
10. 已知 $a$ ， $b$ 为实数，且 $a b$ =1， $a$ $\neq$ 1，设M= $\frac{a}{a + 1} + \frac{b}{b + 1}$ ，N= $\frac{1}{a + 1} + \frac{1}{b + 1}$ ，则M，N的大小关系是（）

A、M＞N B、M=N C、M＜N D、无法确定

查看试题解析

二、填空题

11. 分解因式m³+2m²+m＝．

查看试题解析
12. 若代数式 $\frac{(x - 2) (x - 3)}{2 x - 6}$ 的值为零，则 $x$ =.

查看试题解析
13. 如图，将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上，如果∠1=27°，那么∠2=°.

查看试题解析
14. 如图，已知AB∥CF，E为DF的中点，若AB=8，CF=5，则BD= ．

查看试题解析
15. 已知正数a，b，c是 $Δ$ ABC三边的长，而且使等式a²-c²+ab-bc=0成立，则 $Δ$ ABC是三角形.

查看试题解析
16. 若（-2x+a）（x-1）的结果中不含x的一次项，则a³=.

查看试题解析
17. 如图，△ABC中，D是BC上一点，若AB＝AC＝CD，AD＝BD，∠ADB的度数为．

查看试题解析
18. 如图所示，在△ABC中，已知点D、 E、F分别为BC，AD，BE的中点．且S_△_ABC=8cm² ，则图中△CEF的面积= ．

查看试题解析
19. 关于x的方程 $\frac{a x + 1}{x - 2}$ =−1的解是正数，则a的取值范围是.

查看试题解析
20. 如图，已知AB=A₁B，在AA₁的延长线上依次取A₂、A₃、A₄、…、A_n ，并依次在三角形的外部作等腰三角形，使A₁C₁=A₁A₂ ， A₂C₂=A₂A₃ ， A₃C₃=A₃A₄ ， …，A_n_﹣₁C_n_﹣₁=A_n_﹣₁A_n.
记∠BA₁A=∠1，∠C₁A₂A₁=∠2，……，以此类推. 若∠B=30°，则∠n=°．

查看试题解析

三、解答题

21. 计算

(1)、先化简再求值： ${(2 a + b)}^{2} - (2 a - b) (a + b) - 2 (a - 2 b) (a + 2 b)$ ，其中 $a = \frac{1}{2}, b = - 2$ ．

(2)、 $(2 a + 3 b - c) (2 a - 3 b + c)$

(3)、先化简再求值： $(1 + b + \frac{b^{2}}{1 - b}) \div \frac{1 + b}{1 - b}$ ，其中b=3．

查看试题解析
22. 解分式方程：

(1)、 $\frac{2 - x}{x - 3} + \frac{1}{3 - x} = 1$ ；

(2)、 $\frac{1}{1 - x^{2}} = \frac{- 3}{x - 1} - \frac{5}{1 + x}$ .

查看试题解析
23. 如图，在正方形网格中，每个小正方形的边长都是1，每个小正方形的顶点叫做格点．网格中有一个格点△ABC（即三角形的顶点都在格点上）．

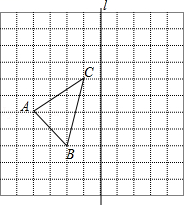
①在图中作出△ABC关于直线l对称的△A₁B₁C₁ （要求A与A₁ ， B与B₁ ， C与C₁相对应）；

②求△ABC的面积；

③在直线l上找一点P，使得△PAC的周长最小．

查看试题解析
24. 如图，在△ABC中，∠ADB＝100°，∠C＝80°，∠BAD＝ $\frac{1}{2}$ ∠DAC，BE平分∠ABC，求∠BED的度数．

查看试题解析
25. 如图，点E、C、D、A在同一条直线上，AB∥DF，ED=AB，∠E=∠CPD．

求证：BC=EF．

查看试题解析
26. 已知：如图，△ABC是等边三角形，BD⊥AC，E是BC延长线上的一点，且∠CED=30°．

(1)、求证：DB=DE．

(2)、在图中过D作DF⊥BE交BE于F，若CF=3，求△ABC的周长．

查看试题解析
27. 某商场计划购进冰箱、彩电进行销售，已知冰箱的进货单价比彩电的进货单价多400元，若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等.该商场冰箱、彩电的售货单价如下表：

冰箱

彩电

售价（元/台）

2500

2000

(1)、分别求出冰箱、彩电的进货单价.

(2)、为了满足市场需求，商场决定用不超过90 000元的资金采购冰箱、彩电共50台。若该商场将购进的冰箱、彩电共50台全部售出，获得利润为w元，为了使商场的利润最大，该商场该如何购进冰箱、彩电，最大利润是多少？

查看试题解析
28. 在△ABC中，AB=AC，D是线段BC的延长线上一点，以AD为一边在AD的右侧作△ADE，使AE=AD，∠DAE=∠BAC，连接CE．

(1)、如图，点D在线段BC的延长线上移动，若∠BAC=40 $^{\circ}$ ，求∠DCE的度数．

(2)、设∠BAC=m，∠DCE=n．
①如图，当点D在线段BC的延长线上移动时，m与n之间有什么数量关系？请说明理由．

②当点D在直线BC上（不与B、C重合）移动时，m与n之间有什么数量关系？请直接写出你的结论．

查看试题解析

	冰箱	彩电
售价（元/台）	2500	2000