广西防城港市2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2018-12-19 类型:期末考试
一、单选题
-
1. “让世界的脚步,在防城港奔跑”,2017中国东盟围际马拉松赛l1月l9日在我市开跑,奖牌以金花茶为立体造型,下面花型设计图,轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某种秋冬流感病毒的直径约为0.000000308米,该直径用科学记数法表示为( )A、 0.308
2. 某种秋冬流感病毒的直径约为0.000000308米,该直径用科学记数法表示为( )A、 0.308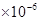 米
B、 3.08
米
B、 3.08 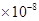 米
C、 3.08
米
C、 3.08 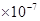 米
D、 3.1
米
D、 3.1 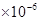 米
3. 已知 =3, =4,则 的值为( )A、12 B、7 C、 D、4. 若分式 有意义,则x应满足的条件是( )A、x≠0 B、x≠3 C、x≥3 D、x≤35. 已知点M(a,1)和点N(-2,b)关于y轴对称,则点N在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 一个三角形三边长分别为l、3、x,且x为整数,则此三角形的周长是( )A、9 B、8 C、7 D、67. 如图,△ABC中,∠C=90 ,∠B=40 .AD是∠BAC的平分线,则∠ADB的度数为( )
米
3. 已知 =3, =4,则 的值为( )A、12 B、7 C、 D、4. 若分式 有意义,则x应满足的条件是( )A、x≠0 B、x≠3 C、x≥3 D、x≤35. 已知点M(a,1)和点N(-2,b)关于y轴对称,则点N在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 一个三角形三边长分别为l、3、x,且x为整数,则此三角形的周长是( )A、9 B、8 C、7 D、67. 如图,△ABC中,∠C=90 ,∠B=40 .AD是∠BAC的平分线,则∠ADB的度数为( )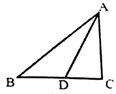 A、 65
A、 65 B、 105
B、 105  C、 100
C、 100  D、 115
D、 115  8. 下列计算正确的是( )A、
8. 下列计算正确的是( )A、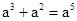 B、
B、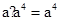 C、
C、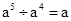 D、
D、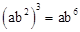 9. 如图,在△ABC中,∠ACB=90 ,∠A=30 ,BC=3cm,点D为AB的中点,则CD的值是( )
9. 如图,在△ABC中,∠ACB=90 ,∠A=30 ,BC=3cm,点D为AB的中点,则CD的值是( )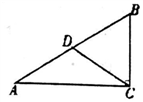 A、3cm B、4cm C、5cm D、6cm10. 下列四个分式中,是最简分式的是( )A、
A、3cm B、4cm C、5cm D、6cm10. 下列四个分式中,是最简分式的是( )A、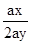 B、
B、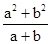 C、
C、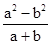 D、
D、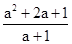 11. 如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=50 ,则∠ABD+∠ACD的值为( )
11. 如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=50 ,则∠ABD+∠ACD的值为( )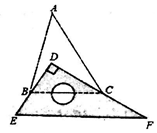 A、 60
A、 60 B、 50
B、 50  C、 40
C、 40  D、 30
D、 30  12. 已知a-b=3,则 的值是( )A、4 B、6 C、9 D、12
12. 已知a-b=3,则 的值是( )A、4 B、6 C、9 D、12二、填空题
-
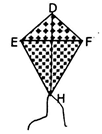
13. 计算: .14. 一个多边形的内角和为720 ,则这个多边形的边数为 .15. 若 ,则n= .16. 小军做了一个如图所示的风筝,其中EH=FH,ED=FD,小军说不用测量就知道DH是EF的垂直平分线.其中蕴含的道理是 .
 17. 如图,△ABC中,点D、E分别是BC,AD的中点,且△ABC的面积为8,则阴影部分的面积是 .
17. 如图,△ABC中,点D、E分别是BC,AD的中点,且△ABC的面积为8,则阴影部分的面积是 .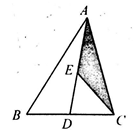 18. 如图,在等边△ABC中.AC=10,点O在AC上,且AO=3,点P是AB上一动点,连接OP,以O为圆心,OP长为半径画弧交BC于一个点D,连接PD,如果PO=PD,那么AP的长是 .
18. 如图,在等边△ABC中.AC=10,点O在AC上,且AO=3,点P是AB上一动点,连接OP,以O为圆心,OP长为半径画弧交BC于一个点D,连接PD,如果PO=PD,那么AP的长是 .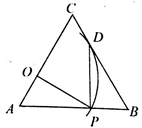
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 分解因式:21. 解分式方程: +1=22. 如图,点D在△ABC的AB边上,且∠ACD=∠A.
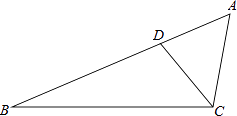 (1)、作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(1)、作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)、在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).23. 先化简,再求值: ,从-1,0,1三个数中选一个合适的数代入求值.24. 从①AB=DC;②BE=CE;③∠B=∠C;④∠BAD=∠CDA四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可). 25. 某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.(1)、求文化官第一批购进书包的单价是多少?(2)、商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?26. 如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.
25. 某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.(1)、求文化官第一批购进书包的单价是多少?(2)、商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?26. 如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.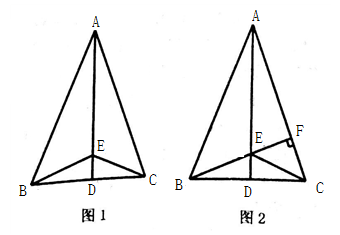 (1)、求证:BE=CE(2)、如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF(3)、在(2)的条件下,若∠BAC=45 ,判断△CFE的形状,并说明理由.
(1)、求证:BE=CE(2)、如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF(3)、在(2)的条件下,若∠BAC=45 ,判断△CFE的形状,并说明理由.