广西北海市合浦县2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2018-12-19 类型:期末考试
一、单选题
-
1. 一个正方形的侧面展开图有( )个全等的正方形.A、2个 B、3个 C、4个 D、6个2. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
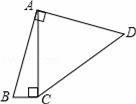 A、y=
A、y= B、y=
B、y=  C、y=
C、y= 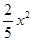 D、y=
D、y= 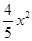 3. 下列命题中,是真命题的是( )
3. 下列命题中,是真命题的是( )①面积相等的两个直角三角形全等;②对角线互相垂直的四边形是正方形;③将抛物线 向左平移4个单位,再向上平移1个单位可得到抛物线 ;
④两圆的半径R、r分别是方程x2-3x+2=0 的两根,且圆心距d=3, 则两圆外切.
A、① B、② C、③ D、④4. 下列命题,其中真命题是( )A、方程x2=x的解是x=1 B、6的平方根是±3 C、有两边和一个角分别对应相等的两个三角形全等 D、连接任意四边形各边中点的四边形是平行四边形5. 如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )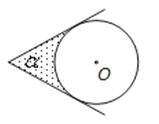 A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于点E,连接AD,则下列结论:①AD⊥BC;②∠EDA=∠B;③OA= AC;④DE是⊙O的切线.其中正确的个数是( )
6. 如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于点E,连接AD,则下列结论:①AD⊥BC;②∠EDA=∠B;③OA= AC;④DE是⊙O的切线.其中正确的个数是( )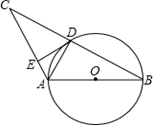 A、1 B、2 C、3 D、47. 下列几何体的主视图既是中心对称图形又是轴对称图形的是( )A、
A、1 B、2 C、3 D、47. 下列几何体的主视图既是中心对称图形又是轴对称图形的是( )A、 B、
B、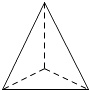 C、
C、 D、
D、 8. 8.已知抛物线y=k(x+1)(x- )与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线有( )A、5条 B、4条 C、3条 D、2条9. 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )
8. 8.已知抛物线y=k(x+1)(x- )与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线有( )A、5条 B、4条 C、3条 D、2条9. 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )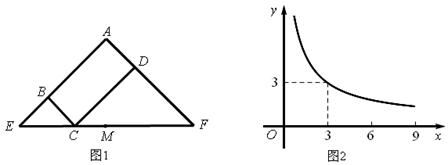 A、当x=3时,EC<EM B、当y=9时,EC>EM C、当x增大时,EC·CF的值增大。 D、当y增大时,BE·DF的值不变。10. 在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、16个 B、15个 C、13个 D、12个11. 对于实数 、 ,定义一种新运算“ ”为: ,这里等式右边是实数运算.例如: .则方程 的解是( )A、 B、 C、x=6 D、
A、当x=3时,EC<EM B、当y=9时,EC>EM C、当x增大时,EC·CF的值增大。 D、当y增大时,BE·DF的值不变。10. 在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、16个 B、15个 C、13个 D、12个11. 对于实数 、 ,定义一种新运算“ ”为: ,这里等式右边是实数运算.例如: .则方程 的解是( )A、 B、 C、x=6 D、 12. 方程x2+2x﹣1=0的根可看出是函数y=x+2与y= 的图象交点的横坐标,用此方法可推断方程x3+x﹣1=0的实根x所在范围为( )A、﹣
12. 方程x2+2x﹣1=0的根可看出是函数y=x+2与y= 的图象交点的横坐标,用此方法可推断方程x3+x﹣1=0的实根x所在范围为( )A、﹣ B、0
B、0  C、
C、 D、
D、 1
1
二、填空题
-
13. 如图①是
 的小方格构成的正方形
的小方格构成的正方形  ,若将其中的两个小方格涂黑,使得涂黑后的整个
,若将其中的两个小方格涂黑,使得涂黑后的整个  图案(含阴影)是轴对称图形,且规定沿正方形
图案(含阴影)是轴对称图形,且规定沿正方形  对称轴翻折能重合的图案都视为同一种,比如图②中四幅图就视为同一种,则得到不同的图案共有种.
对称轴翻折能重合的图案都视为同一种,比如图②中四幅图就视为同一种,则得到不同的图案共有种. 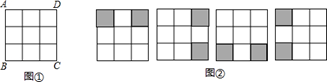 14. 从 这七个数中,随机取出一个数,记为 ,那么 使关于 的方程 有整数解,且使关于 的不等式组 有解的概率为.15. 已知若分式 的值为0,则x的值为 .16. 计算:3x(4y+1)的结果为
14. 从 这七个数中,随机取出一个数,记为 ,那么 使关于 的方程 有整数解,且使关于 的不等式组 有解的概率为.15. 已知若分式 的值为0,则x的值为 .16. 计算:3x(4y+1)的结果为三、解答题
-
17. 计算:(1)、﹣ m2n•(﹣mn2)2(2)、(x2﹣2x)(2x+3)÷(2x)(3)、(2x+y)(2x﹣y)+(x+y)2﹣2(2x2+xy)(4)、(ab﹣b2) .18. 用适当的方法解下列方程:(1)、2x2﹣8x=0.(2)、x2﹣3x+4=0.(3)、y= x2﹣x+3,求出抛物线的开口方向、对称轴、顶点坐标.19. 用适当的方法解下列方程:(1)、x2=3x(2)、2x2﹣x+6=0.(3)、y2+3=2 y;(4)、x2+2x+120=0.20. 某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变).(1)、从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?(2)、因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.21. 某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)、2014年这种礼盒的进价是多少元/盒?
(2)、若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?