2016-2017学年湖北省荆州市五县市区高三上学期期末数学试卷（理科）

试卷更新日期：2017-04-01 类型：期末考试

进入出卷网下载

一、选择题

1. 若集合A={x|1≤2^x≤16}，B={x|log₃（x²﹣2x）＞1}，则A∩B等于（）

A、（3，4] B、[3，4] C、（﹣∞，0）∪（0，4] D、（﹣∞，﹣1）∪（0，4]

查看试题解析
2. 计算sin46°•cos16°﹣cos314°•sin16°=（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{2}$

查看试题解析
3. 已知tan（α﹣ $\frac{π}{4}$ ）= $\frac{1}{2}$ ，则 $\frac{\sin α + \cos α}{\sin α - \cos α}$ 的值为（）

A、 $\frac{1}{2}$ B、2 C、2 $\sqrt{2}$ D、﹣2

查看试题解析
4. 设命题p：∃x₀∈（0，+∞）， $3^{x_{0}} < x_{0}^{3}$ ，则命题p的否定为（）

A、∀x∈（0，+∞），3^x＜x³ B、∀x∈（0，+∞），3^x＞x³ C、∀x∈（0，+∞），3^x≥x³ D、∃x∈（0，+∞），3^x≥x³

查看试题解析
5. 已知实数x，y满足 ${\begin{matrix} y \geq x + 2 \\ x + y \leq a \\ x \geq 1 \end{matrix}$ ，其中a= $\int_{0}^{3}$ （x²﹣1）dx，则实数 $\frac{y}{x + 1}$ 的最小值为（）

A、 $\frac{3}{2}$ B、 $\frac{5}{2}$ C、 $\frac{2}{3}$ D、 $\frac{4}{3}$

查看试题解析
6. 设向量 $\vec{O A} = \vec{e_{1}} ， \vec{O B} = \vec{e_{2}}$ ，若 $\vec{e_{1}}$ 与 $\vec{e_{2}}$ 不共线，且 $\vec{A P} = 6 \vec{P B}$ ，则 $\vec{O P}$ =（）

A、 $\frac{1}{7} \vec{e_{1}} - \frac{6}{7} \vec{e_{2}}$ B、 $\frac{6}{7} \vec{e_{1}} - \frac{1}{7} \vec{e_{2}}$ C、 $\frac{1}{7}$ $\vec{e_{1}}$ + $\frac{6}{7}$ $\vec{e_{2}}$ D、 $\frac{6}{7} \vec{e_{1}} + \frac{1}{7} \vec{e_{2}}$

查看试题解析
7. 已知函数 $f (x) = \sin (\frac{1}{4} x + \frac{π}{6}) (x \in R)$ ，把函数f（x）的图象向右平移 $\frac{8 π}{3}$ 个单位得函数g（x）的图象，则下面结论正确的是（）

A、函数g（x）是奇函数 B、函数g（x）在区间[π，2π]上是增函数 C、函数g（x）的最小正周期是4π D、函数g（x）的图象关于直线x=π对称

查看试题解析
8. 在一球面上有A，B，C三点，如果AB=4 $\sqrt{3} ， ∠ A C B = 60^{\circ}$ ，球心O到平面ABC的距离为3，则球O的表面积为（）

A、36π B、64π C、100π D、144π

查看试题解析
9. 如图程序框图的算法思路，源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法，执行该程序框图，若输入的n，a_n ， x分别为5，1，﹣2，且a₄=5，a₃=10，a₂=10，a₁=5，a₀=1，则输出的v=（）

A、1 B、2 C、﹣1 D、﹣2

查看试题解析
10. 某三棱锥的三视图如图所示，其侧（左）视图为直角三角形，则该三棱锥最长的棱长等于（）

A、 $4 \sqrt{2}$ B、 $\sqrt{34}$ C、 $\sqrt{41}$ D、 $5 \sqrt{2}$

查看试题解析
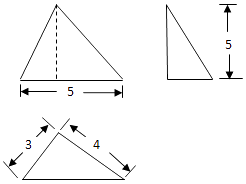11. 已知O，F分别为双曲线E： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的中心和右焦点，点G，M分别在E的渐近线和右支，FG⊥OG，GM∥x轴，且|OM|=|OF|，则E的离心率为（）

A、 $\frac{\sqrt{5}}{2}$ B、 $\frac{\sqrt{6}}{2}$ C、 $\frac{\sqrt{7}}{2}$ D、 $\sqrt{2}$

查看试题解析
12. 设定义在（0，+∞）的函数f（x）的导函数是f'（x），且x⁴f'（x）+3x³f（x）=e^x ， $f (3) = \frac{e^{3}}{81}$ ，则x＞0时，f（x）（）

A、有极大值，无极小值 B、有极小值，无极大值 C、既无极大值，又无极小值 D、既有极大值，又有极小值

查看试题解析

二、填空题．

13. 正△ABC中， $\vec{A B}$ 在 $\vec{B C}$ 方向上的投影为﹣1，且 $\vec{A D} = 2 \vec{D C}$ ，则 $\vec{B D} \cdot \vec{A C}$ = ．

查看试题解析
14. 已知数列{a_n}的前n项和为S_n ，且满足4S_n=a_n+1（n∈N^*），设b_n=log₃|a_n|，则数列{b_n}的通项公式为．

查看试题解析
15. 在三棱锥A﹣BCD中，△ABC与△BCD都是边长为6的正三角形，平面ABC⊥平面BCD，则该三棱锥的外接球的面积为．

查看试题解析
16. 若函数f（x）=（e^x+ae^﹣^x）sinx为奇函数，则a= ．

查看试题解析

三、解答题。

17. 已知a，b，c分别为锐角△ABC三个内角A，B，C的对边，且（a+b）（sinA﹣sinB）=（c﹣b）sinC
（Ⅰ）求∠A的大小；
（Ⅱ）若f（x）= $\sqrt{3}$ sin $\frac{x}{2}$ •cos $\frac{x}{2}$ +cos² $\frac{x}{2}$ ，求f（B）的取值范围．

查看试题解析
18. 已知等差数列{a_n}的前n项和为S_n ，且S₆=5S₂+18，a_3n=3a_n ，数列{b_n}满足b₁•b₂•…•b_n=4^Sn ．
（Ⅰ）求数列{a_n}，{b_n}的通项公式；
（Ⅱ）令c_n=log₂b_n ，且数列 ${\frac{1}{c_{n} \cdot c_{n + 1}}}$ 的前n项和为T_n ，求T₂₀₁₆ ．

查看试题解析
19. 在三棱柱ABCA₁B₁C₁中，侧面ABB₁A₁为矩形，AB=3，AA₁=3 $\sqrt{2}$ ，D为AA₁的中点，BD与AB₁交于点O，CO⊥侧面ABB₁A₁ ．
（Ⅰ）证明：BC⊥AB₁；
（Ⅱ）若OC=OA，求二面角A₁﹣AC﹣B的余弦值．

查看试题解析
20. 已知抛物线E：y²=2px（p＞0）的焦点为F，过F且垂直于x轴的直线与抛物线E交于A，B两点，E的准线与x轴交于点C，△CAB的面积为4，以点D（3，0）为圆心的圆D过点A，B．
（Ⅰ）求抛物线E和圆D的方程；
（Ⅱ）若斜率为k（|k|≥1）的直线m与圆D相切，且与抛物线E交于M，N两点，求 $\vec{F M} \cdot \vec{F N}$ 的取值范围．

查看试题解析
21. 已知a∈R，函数f（x）=ln（x+a）﹣x，曲线y=f（x）与x轴相切．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）是否存在实数m使得 $\frac{f (x)}{x} > m (1 - e^{x})$ 恒成立？若存在，求实数m的值；若不存在，说明理由．

查看试题解析
22. 在直角坐标系xOy中，圆C的参数方程 ${\begin{matrix} x = 1 + \cos ϕ \\ y = \sin ϕ \end{matrix}$ （φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．

(1)、求圆C的极坐标方程；

(2)、直线l的极坐标方程是2ρsin（θ+ $\frac{π}{3}$ ）=3 $\sqrt{3}$ ，射线OM：θ= $\frac{π}{3}$ 与圆C的交点为O、P，与直线l的交点为Q，求线段PQ的长．

查看试题解析
23. 已知函数f（x）=|x+2|﹣2|x﹣1|．
（Ⅰ）求不等式f（x）≥﹣2的解集M；
（Ⅱ）对任意x∈[a，+∞），都有f（x）≤x﹣a成立，求实数a的取值范围．

查看试题解析