江苏省无锡市南长实验、侨谊教育集团2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2018-11-17 类型：期中考试
一、单选题
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 在下列各组数据中，不能作为直角三角形的三边的是 （ ）A、3，4，6 B、7，24，25 C、6，8，10 D、9，12，153. 如图所示，△ABC ≌△AEF，AB=AE，∠B=∠E，有以下结论：①AC=AF；②∠FAB=∠EAB；③EF=BC；④∠EAB=∠FAC，其中正确的个数是 （ ）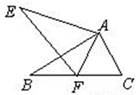
A、1个 B、2个 C、3个 D、4个4. 一个等腰三角形的两边长分别是4和9，则它的周长是（ ）A、13 B、17 C、22 D、17或225. 请仔细观察用直尺和圆规作一个角等于已知角的示意图，请你根据所学的三角形全等有关的知识，说明画出∠A′O′B′=∠AOB的依据是（ ）
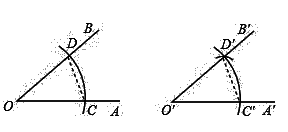A、SAS B、ASA C、AAS D、SSS6. 联欢会上，A，B，C三名选手站在一个三角形三个顶点上玩抢凳子游戏，在他们中间放个木凳，谁先抢到凳子就获胜，为使游戏公平，凳子应放的最适当位置是△ABC的 （ ）A、三边中线的交点 B、三边中垂线的交点 C、三条角平分线的交点 D、三边上高的交点7. 如图，△ABC中，AB=5，AC=8，BD，CD分别平分∠ABC，∠ACB，过点D作直线平行于BC，分别交AB，AC于E，F，则△AEF的周长为 （ ）
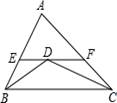A、12 B、13 C、14 D、188. 如图，BD是∠ABC平分线，DE AB于E，AB=36cm，BC=24cm，S△ABC =144cm2 ， DE为（ ）
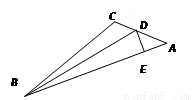A、4.8cm B、4.5cm C、4 cm D、2.4cm9. 如图，点P、Q分别是边长为4cm的等边△ABC边AB，BC上的动点，点P从顶点A，点Q从顶点B同时出发，且速度都为1cm/s，连接AQ、CP交于点M，下面四个结论：①BP＝CM；②△ABQ≌△CAP；③∠CMQ的度数不变，始终等于60°；④当第 秒或第 秒时，△PBQ为直角三角形，正确的有几个 （ ）
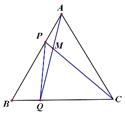A、1 B、2 C、3 D、410. 如图，AO OM，OA=8，点B为射线OM上的一个动点，分别以OB、AB为直角边，B为直角顶点，在OM两侧作等腰Rt△OBF、等腰Rt△ABE，连接EF交OM于P点，当点B在射线OM上移动时，PB的长度是 （ ）
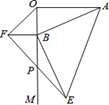A、3.6 B、4 C、4.8 D、PB的长度随B点的运动而变化二、填空题
-
11. 已知直角三角形的两条直角边长分别是6和8，则斜边上的中线长 ．12. 如图，在△ABC中，∠ABC＝90°，∠A＝50°，CD＝CB，∠ABD＝ ．
13. 如图，∠1=∠2，要使△ABE≌△ACE，需添加一个条件是（填上一个条件即可）．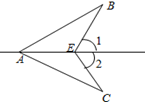
14. 如图，图中的所有三角形都是直角三角形，所有四边形都是正方形，正方形A的边长为 ，另外四个正方形中的数字8，x，10，y分别表示该正方形面积，则x与y的数量关系是.
15. 如图，已知△ABC为等腰直角三角形，D为斜边AB上任意一点，（不与点A、B重合），连接CD，作EC⊥DC，且EC=DC，连接AE，则∠EAC为度.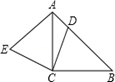
16. 在三角形ABC中，AB=AC，D是底边上的中点，BE垂直AC于点E，①∠ABC=∠ACB；②AD⊥BC；③∠BAD=∠CBE；④AB=2BD，其中正确的有.
17. 在一个长为8分米，宽为5分米，高为7分米的长方体上，截去一个长为6分米，宽为5分米，深为2分米的长方体后，得到一个如图所示的几何体. 一只蚂蚁要从该几何体的顶点A处，沿着几何体的表面到几何体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是分米．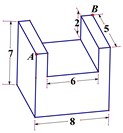
18. 如图，Rt△ABC中，∠C=90°，点P为AC边上的一点，延长BP至点D，使得AD=AP，当AD⊥AB时，过D作DE⊥AC于E，AB－BC=4，AC=8，则△ABP面积为.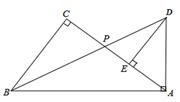
三、解答题
-
19. 如图，在10×10的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）.
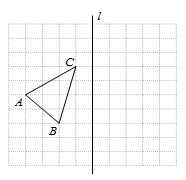(1)、在图中作出△ABC关于直线l对称的△A1B1C1；（要求：A与A1 ， B与B1 ， C与C1相对应）(2)、若有一格点P到点A、B的距离相等（PA=PB），则网格中满足条件的点P共有个.20. 如图，四边形ABCD的对角线AC与BD相交于点O，∠1＝∠2，∠3＝∠4．
求证：
(1)、△ABC≌△ADC；(2)、OB＝OD．21. 如图，已知点D为OB上的一点，请用直尺和圆规按下列要求进行作图，保留作图痕迹．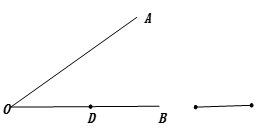
(1)、作∠AOB的平分线OC；(2)、在OC上取一点P，使得OP=a ；(3)、爱动脑筋的小刚经过仔细观察后，进行如下操作：在边OA上取一点E，使得PE＝PD，这时他发现∠OEP与∠ODP之间存在一定的数量关系，请写出∠OEP与∠ODP的数量关系，并说明理由．
22. 如图，在△ABC中，AB=AC，AC的垂直平分线分别交BC、AC于点D、E．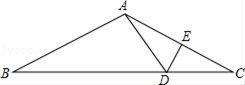
(1)、若AC=12，BC=15，求△ABD的周长；(2)、若∠B=20°，求∠BAD的度数．23. 如图，在梯形ABCD中，AD∥BC，E为CD中点，连接AE并延长AE交BC的延长线于点F．
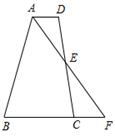(1)、求证：CF =AD；(2)、若AD=2，AB=8，当BC为多少时，点B在线段AF的垂直平分线上？说明理由.24. 如图：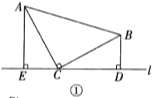
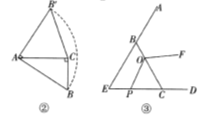(1)、观察推理：如图①，在△ABC中，∠ACB=90°，AC=BC，直线l过点C，点A、B在直线l的同侧，垂足分别为.求证：△AEC≌△CDB．(2)、类比探究：如图②，在Rt△ABC中，∠ACB=90°，AC=4，将斜边AB绕点A逆时针旋转90°至AB ， ， 连接CB ， ， 求△ACB ， 的面积.(3)、拓展提升：如图③，在△EBC中，∠E=∠ECB=60°，EC=BC=3，点O在BC上，且OC=2，动点P从点E沿射线EC以每秒1个单位长度的速度运动，连接OP，将线段OP绕点O逆时针旋转120°得到线段OF.要使点 F恰好落在射线EB上，求点P运动的时间t.25. 如图，△ABC中，∠C=90°，AB=10cm，BC=6cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．
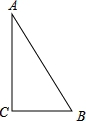(1)、出发2秒后，求△ABP的面积；(2)、当t为几秒时，BP平分∠ABC ；(3)、问t为何值时，△BCP为等腰三角形？(4)、另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？