江苏省江阴市长泾片2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2018-11-17 类型:期中考试
一、单选题
-
1. 在一些汉字的美术字中,有的是轴对称图形.下面四个美术字中可以看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法正确的是( )A、无限小数都是无理数 B、9的立方根是3 C、平方根等于本身的数是0 D、数轴上的每一个点都对应一个有理数3. 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
2. 下列说法正确的是( )A、无限小数都是无理数 B、9的立方根是3 C、平方根等于本身的数是0 D、数轴上的每一个点都对应一个有理数3. 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )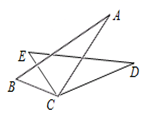 A、AB=DE B、∠B=∠E C、AC=DC D、∠A=∠D4. 下列四组线段中,可以构成直角三角形的是( )A、4,5,6 B、2,3,4 C、
A、AB=DE B、∠B=∠E C、AC=DC D、∠A=∠D4. 下列四组线段中,可以构成直角三角形的是( )A、4,5,6 B、2,3,4 C、 ,3,4
D、 1,
,3,4
D、 1, 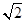 ,3
5. 如图是一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )
,3
5. 如图是一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )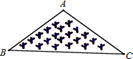 A、△ABC三条中线的交点 B、△ABC三边的垂直平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三条角平分线的交点6. 如图,正方形网格中的每个小正方形边长都是1.已知A、B是两格点,若△ABC为等腰三角形,且S△ABC=1.5,则满足条件的格点C有( )
A、△ABC三条中线的交点 B、△ABC三边的垂直平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三条角平分线的交点6. 如图,正方形网格中的每个小正方形边长都是1.已知A、B是两格点,若△ABC为等腰三角形,且S△ABC=1.5,则满足条件的格点C有( )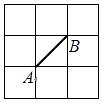 A、1个 B、2个 C、3个 D、4个7. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG.若△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
A、1个 B、2个 C、3个 D、4个7. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG.若△ADG和△AED的面积分别为50和39,则△EDF的面积为( )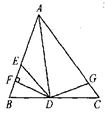 A、11 B、5.5 C、7 D、3.58. 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB= S矩形ABCD , 则点P到A、B两点距离之和PA+PB的最小值为( )
A、11 B、5.5 C、7 D、3.58. 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB= S矩形ABCD , 则点P到A、B两点距离之和PA+PB的最小值为( )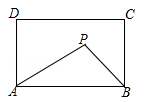 A、
A、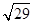 B、
B、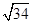 C、
C、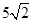 D、
D、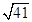
二、填空题
-
9. 的算术平方根是 ,﹣2的相反数是 ,的绝对值是 .10. 若式子 有意义,则x的取值范围为 .11. 若 ,则以 为边长的等腰三角形的周长为 .12. 若等腰三角形的一个内角为50°,则它的底角是 .13. 在等腰直角△ABC中,其顶角平分线长为6,则△ABC的面积为 .14. 如图,△ABC≌△ADE,∠EAC=40°,则∠B=°.
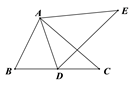 15. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,则∠C的度数为 .
15. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,则∠C的度数为 .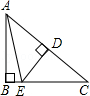 16. 如图,在△ABC中,AB=AC,BC=6,△DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF= .
16. 如图,在△ABC中,AB=AC,BC=6,△DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF= .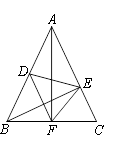 17. 如图,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是 .
17. 如图,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是 . 18. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为 .
18. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为 .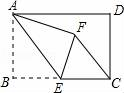
三、解答题
-
19.(1)、解方程: ;(2)、计算: + -( )2;20. 已知某正数的两个平方根分别是 和 , 的立方根是 .
求 的算术平方根.
21. 如图,已知:AB=AD,BC=CD,AE⊥BC,垂足为E,AF⊥CD,垂足为F.
求证:
(1)、∠B=∠D;(2)、AE=AF.22. 如图,在△ABC中,AC=6,BC=8,AB=10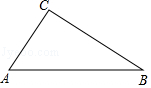 (1)、尺规作图:作AD平分∠CAB,交BC于点D;(2)、求CD的长度.23. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.
(1)、尺规作图:作AD平分∠CAB,交BC于点D;(2)、求CD的长度.23. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.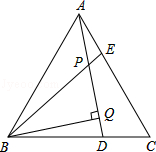 (1)、求证:△ADC≌△BEA;(2)、若PQ=4,PE=1,求AD的长.24. 如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,BC=5cm,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△ABP为等腰三角形?
(1)、求证:△ADC≌△BEA;(2)、若PQ=4,PE=1,求AD的长.24. 如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,BC=5cm,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△ABP为等腰三角形?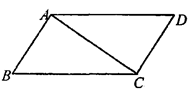 25. 如图:
25. 如图: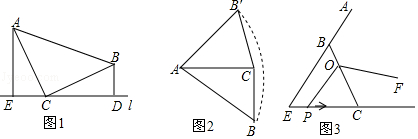 (1)、观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;(2)、类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.(3)、拓展提升:如图3,等边△EBC中,EC=BC=4cm,点O在BC上,且OC=3cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.26. 在四边形ABDE中,C是BD边的中点.
(1)、观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;(2)、类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.(3)、拓展提升:如图3,等边△EBC中,EC=BC=4cm,点O在BC上,且OC=3cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.26. 在四边形ABDE中,C是BD边的中点.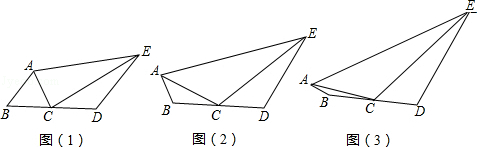 (1)、如图(1),若AC平分∠BAE,∠ACE=90°,则线段AE、AB、DE的长度满足的数量关系为;(直接写出答案)(2)、如图(2),AC平分∠BAE,EC平分∠AED,若∠ACE=120°,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明;(3)、如图(3),BD=8,AB=2,DE=8,若ACE=135°,则线段AE长度的最大值是(直接写出答案).
(1)、如图(1),若AC平分∠BAE,∠ACE=90°,则线段AE、AB、DE的长度满足的数量关系为;(直接写出答案)(2)、如图(2),AC平分∠BAE,EC平分∠AED,若∠ACE=120°,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明;(3)、如图(3),BD=8,AB=2,DE=8,若ACE=135°,则线段AE长度的最大值是(直接写出答案).