江苏省江阴市澄要片2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2018-11-17 类型：期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列各数属于无理数的是（ ）A、3.14159 B、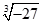
C、
D、
3. 如图，下列条件中，不能证明△ABD≌△ACD的是（ ）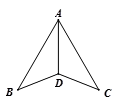
A、AB＝AC ，BD＝CD B、∠B＝∠C，∠BAD＝∠CAD C、∠B＝∠C，BD＝CD D、∠ADB＝∠ADC，DB＝DC4. 已知△ABC中，a、b、c分别是∠A，∠B，∠C的对边，下列条件不能判断△ABC是直角三角形的是 （ ）A、∠A＝∠C－∠B B、a2＝b2－c2 C、a：b：c＝2：3：4 D、 a＝
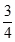，b＝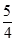 
，c＝1
5. 由四舍五入法得到的近似数8.30万，它是精确到（ ）位．A、精确到百分位 B、精确到百位 C、精确到千位 D、精确到万位6.如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是（ ）
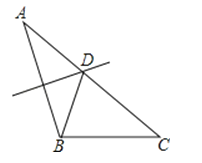A、8 B、9 C、10 D、117. 如图，在Rt△ABC中，AB＝9，BC＝6，∠B＝90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）
A、
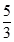B、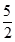
C、4
D、5
8. 如图，D是△ABC中BC边上一点，AB=AC=BD，则∠1和∠2的关系是（ ）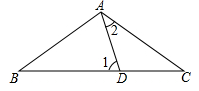
A、180°+∠2=3∠1 B、∠1+∠2=90° C、180°－∠1=3∠2 D、∠1=2∠29. 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为40和28，则△EDF的面积为（ ）
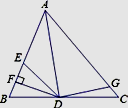A、12 B、6 C、7 D、810. 如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD=2∠ACB．若AF=50，EC=7，则DE的长为（ ）
A、14 B、21 C、24 D、25二、填空题
-
11. 二次根式 有意义的条件是12. 若实数m，n满足(m－1)2 + =0，则m+2n= ．13. 如图，△ABC中，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G，∠BAC=128°，∠EAG= °.
14. 若直角三角形斜边上的高和中线长分别是4cm，6cm，则它的面积是cm2 ．15. 若等腰三角形的一个内角为50°，则它的底角是 ．16. 如图，AB＝12，AB⊥BC于点B， AB⊥AD于点A，AD＝5，BC＝10，E是CD的中点，则AE的长是 ．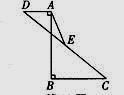
17. 如图，在△ABC中，∠C=90°，AC=3，BC=4，点O是BC中点，将△ABC绕点O旋转得△A′B' C′，则在旋转过程中点A、C′两点间的最大距离是.
三、解答题
-
18.(1)、解方程：4x2-81=0；(2)、计算： ＋ －( )2；19. 已知2x—y的平方根为±3，3x＋y的立方根是1，求3x－2y的平方根．20. 有理数a、b、c在数轴上的位置如图所示，化简
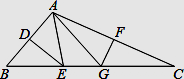
21. 如图，∠A=∠D=90°，AC=DB，AC、DB相交于点O．求证：OB=OC．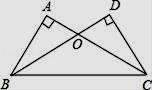
22. 如图，在△ABC中，点D在边AC上，DB=BC，E是CD的中点，F是AB的中点，求证：EF= AB．
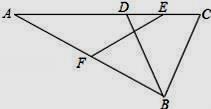23. 如图，在△ABC的一边AB上有一点P．
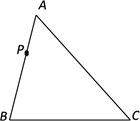(1)、能否在另外两边AC和BC上各找一点M、N，使得△PMN的周长最短．若能，请画出点M、N的位置，若不能，请说明理由；(2)、若∠ACB=40°，在（1）的条件下，求出∠MPN的度数．24. 已知如图，在矩形ABCD中，AB=4cm，BC=7cm，
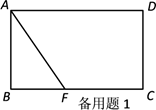
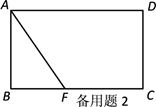
(1)、点F在边BC上，且 BF=3，若点P从点A出发，以每秒1cm的速度沿A→D→C→F运动，设点P运动的时间为t秒，求当t为何值时，△AFP为等腰三角形？
(2)、如图2，将长方形ABCD折叠，折痕为MN，点A的对应点A′落在线段BC上，当点A′ 在BC上移动时，点M、N也随之移动，若限定点M、N分别在线段AB、AD上移动，则点A′ 在线段BC上可移动的最大距离是 ．
25. 如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）