江苏省东台市第七联盟2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2018-11-17 类型:期中考试
一、单选题
-
1. 下列汽车标志中是轴对称图形的有( )
 A、5个 B、4个 C、3个 D、2个2. 下列实数中, (相邻两个3之间依次增加一个2),无理数的个数是( )A、2个 B、3个 C、4个 D、5个3. 如图,给出下列四组条件:
A、5个 B、4个 C、3个 D、2个2. 下列实数中, (相邻两个3之间依次增加一个2),无理数的个数是( )A、2个 B、3个 C、4个 D、5个3. 如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E.BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
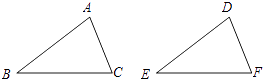 A、1组 B、2组 C、3组 D、4组4. 下列四组数中不是勾股数的一组是( )A、4,5,6 B、7,24,25 C、5,12,13 D、11,60,615. 对于四舍五入得到的近似数 ,下列说法正确的是( )A、精确到百位 B、精确到个位 C、精确到万位 D、精确到百分位6. 如图,AB⊥AC,AD⊥BC,垂足为D,AB=3,AC=4,AD= ,BD= ,则点B到直线AD的距离为( )
A、1组 B、2组 C、3组 D、4组4. 下列四组数中不是勾股数的一组是( )A、4,5,6 B、7,24,25 C、5,12,13 D、11,60,615. 对于四舍五入得到的近似数 ,下列说法正确的是( )A、精确到百位 B、精确到个位 C、精确到万位 D、精确到百分位6. 如图,AB⊥AC,AD⊥BC,垂足为D,AB=3,AC=4,AD= ,BD= ,则点B到直线AD的距离为( )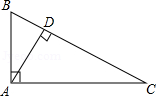 A、
A、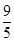 B、
C、3
D、4
7. 在等腰三角形ABC中,AB=AC=8cm,腰AB的垂直平分线交另一腰AC于D,若△BCD的周长为10cm,则底边BC的长为( )
B、
C、3
D、4
7. 在等腰三角形ABC中,AB=AC=8cm,腰AB的垂直平分线交另一腰AC于D,若△BCD的周长为10cm,则底边BC的长为( )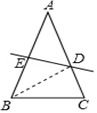 A、1cm B、2cm C、3cm D、4 cm8. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A、1cm B、2cm C、3cm D、4 cm8. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )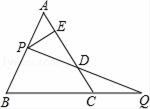 A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题
-
9. 若等腰三角形的一个角为70゜,则其顶角的度数为 .10. 若实数a、b满足|a+2|+ =0,则 = .11. 已知一个直角三角形的两边长分别为5cm和12cm,则第三边为 .12. 如图,已知Rt△ABC中,∠ACB=90°,D是AB的中点, CD=5cm,则AB=cm.
 13. 如图,是4×4正方形网格,其中已有4个小方格涂成了黑色.现在要从其余白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有种选择.
13. 如图,是4×4正方形网格,其中已有4个小方格涂成了黑色.现在要从其余白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有种选择.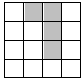 14. 如图,等边△ABC的两条中线BD、CE交于点O,则∠BOC= °.
14. 如图,等边△ABC的两条中线BD、CE交于点O,则∠BOC= °.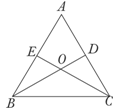 15. 已知正数
15. 已知正数 的两个不同的平方根是
的两个不同的平方根是 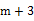 和
和 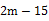 ,则
,则  = .
16. 如图,OP=1,过P作PP1⊥OP,得OP1= ;再过P1作P1P2⊥OP1且P1P2=1,得OP2= ;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;……依此法继续作下去,得OP2016= .
= .
16. 如图,OP=1,过P作PP1⊥OP,得OP1= ;再过P1作P1P2⊥OP1且P1P2=1,得OP2= ;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;……依此法继续作下去,得OP2016= .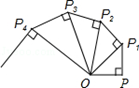 17. 如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 .
17. 如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 .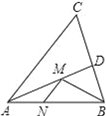
三、解答题
-
18.(1)、(2)、 ;19. 如图所示,要在公园(四边形ABCD)中建造一座音乐喷泉,喷泉位置应符合如下要求:
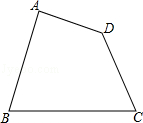
( 1 )到公园两个出入口A、C的距离相等;
( 2 )到公园两边围墙AB、AD的距离相等;
请你用尺规作图的方法确定喷泉的位置P.(不必写作法,但要保留作图痕迹)
20. 如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F.求证:DE=DF.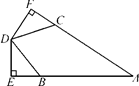 21. 如图,在△ABC中,AB=20,AC=15,BC=25,AD⊥BC,垂足为D.求AD,BD的长.
21. 如图,在△ABC中,AB=20,AC=15,BC=25,AD⊥BC,垂足为D.求AD,BD的长.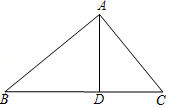 22. 如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DF⊥BE,垂足是F,求证:BF=EF.
22. 如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DF⊥BE,垂足是F,求证:BF=EF.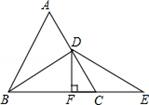 23. 已知2b+3的平方根是 ,3a+2b+1的算术平方根为4,
23. 已知2b+3的平方根是 ,3a+2b+1的算术平方根为4,求:
(1)、3a+6b的立方根;(2)、已知a=5, ,求 .24. 如图,将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE,连接BE,延长DE、BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.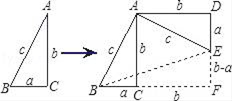 (1)、判断△ABE的形状,并证明你的结论;(2)、用含b代数式表示四边形ABFE的面积;(3)、求证:a2+b2=c2 .25. 阅读下面材料,并解决问题:(1)、如图(1),等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5欲求∠APB的度数,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(1)、判断△ABE的形状,并证明你的结论;(2)、用含b代数式表示四边形ABFE的面积;(3)、求证:a2+b2=c2 .25. 阅读下面材料,并解决问题:(1)、如图(1),等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5欲求∠APB的度数,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.请将下列解题过程补充完整。
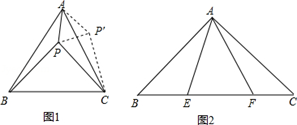
∵△ACP′≌△ABP,
∴AP′==3,CP′==4,∠=∠APB.
由题意知旋转角∠PA P′=60°,∴△AP P′为 三角形,
P P′=AP=3,∠A P′P=60°。
易证△P P′C为直角三角形,且∠P P′C=90°,
∴∠APB=∠AP′C=∠A P′P+∠P P′C=°+°=°.
(2)、请你利用第(1)题的解答思想方法,解答下面问题:已知如图(2),△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,
求证:EF2=BE2+FC2 .