江苏省常州市2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2018-11-17 类型：期中考试
一、单选题
-
1. 以下是小明收集的四个轴对称图案，他收集错的是（ ）A、
B、
C、
D、
2. 下列说法错误的是（ ）A、两个面积相等的圆一定全等 B、全等三角形是指形状、大小都相同的三角形 C、斜边上中线和一条直角边对应相等的两直角三角形全等 D、底边相等的两个等腰三角形全等3. 三角形具有稳定性，就是当三角形的三边长确定时，三角形的形状和大小就确定了，其理论依据是（ ）A、SAS B、ASA C、AAS D、SSS4. 已知△ABC中，a、b、c分别是∠A，∠B，∠C的对边，下列条件不能判断△ABC是直角三角形的是（ ）A、∠A﹣∠B=∠C B、∠A：∠B：∠C=3：4：5 C、（b+c）（b﹣c）=a2 D、a=7，b=24，c=255. 在联欢会上，有A，B，C三名选手站在一个三角形的三个顶点位置上，他们在玩“抢凳子”游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在△ABC的（ ）A、三边中垂线的交点 B、三边中线的交点 C、三条角平分线的交点 D、三边上高的交点6. 如图，将矩形 沿折痕 折叠，使点 落在 上的 处，已知 ， 的面积是24，则 等于（ ）
A、1 B、2 C、3 D、47. 如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E，且PE＝3，AP＝5，点F在边AB上运动，当运动到某一位置时△FAP面积恰好是△EAP面积的2倍，则此时AF的长是（ ）
A、10 B、8 C、6 D、48. 如图，在 中 ， 于点 ， 于点 ， 为 边的中点，连接 、 ，则下列结论：① ；② 为等边三角形.下面判断正确是（ ）
A、①正确 B、②正确 C、①②都正确 D、①②都不正确二、填空题
-
9. 已知△ABC≌△DEF，∠A=30°，∠E=50°，则∠C= ．10. 若直角三角形的两条直角边长分别为6和8，则斜边长为 ．
11. 如图，已知AB∥CF，E为DF的中点，若AB=8，CF=5，则BD= ．
12. 如图，△ABC中，∠A=∠ABC，AC=6，BD⊥AC于点D，E为BC的中点，连接DE．则DE= ．
13. 青青同学把一张长方形纸折了两次，如图，使点A，B都落在DG上，折痕分别是DE，DF，则∠EDF的度数为 ．
14. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连结AA′，若∠AA′B′=20°，则∠B的度数为°．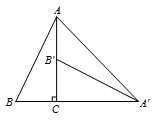
15. 如图，DE是△ABC中AC边上的垂直平分线，若BC=9，AB=11，则△EBC的周长为 ．
16. 如图，是由直角三角形和正方形拼成的图形，正方形A的边长为5，另外四个正方形中的数字4，x，6，y分别表示该正方形面积，则x与y的数量关系是.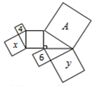
17. 如图，一等腰三角形的周长为16，底边上的高是4，则此三角形的底边长是.
18. 如图，将矩形纸片ABCD折叠，B、C两点恰好重合落在AD边上点P处，已知 ，PM=3，PN=4，那么矩形纸片ABCD的面积为 ．
三、解答题
-
19. 如图，在正方形网格上有一个△DEF（顶点在格点上）．
(1)、①画△DEF关于直线HG的轴对称图形；②画△DEF的边EF上的高所在直线；
(2)、若网格上的最小正方形边长为1，求△DEF的面积．20. 在3×3的正方形格点图中，有格点△ABC和格点△DEF，且△ABC和△DEF关于某直线成轴对称，请分别在下面四个图中各画出1个这样的△DEF，要求四个图互不一样．
21. 如图，点B、E、C、F在同一条直线上，∠A=∠D，∠B=∠DEF，BE=CF．求证：AC=DF．
22. 如图，在△ABC中，∠ACB=90
，AC=BC，AE是BC边的中线，过点C作CF⊥AE，垂足为F，过点B作BD⊥BC交CF的延长线于点D． 
(1)、试说明：AE=CD；(2)、若AC=12cm，求BD的长．23. 如图，花果山上有两只猴子在一棵树CD上的点B处，且BC=5m，它们都要到A处吃东西，其中一只猴子甲沿树爬下走到离树10m处的池塘A处，另一只猴子乙先爬到树D处后再沿缆绳DA线段滑到A处．已知两只猴子所经过的路程相等，设BD为xm．
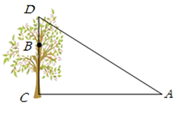(1)、请用含有x的整式表示线段AD的长为m；(2)、求这棵树高有多少米？24. 如图，△ABC中，∠ABC、∠ACB的平分线相交于点P，过点P且平行于BC的直线分别交AB、AC于点D、点E．
(1)、求证：DB＝DP；(2)、若DB＝5，DE＝9，求CE的长．25. 在如图所示的网格中有四条线段AB、CD、EF、GH（线段端点在格点上），
(1)、选取其中三条线段，使得这三条线段能围成一个直角三角形．答：选取的三条线段为 ．
(2)、只变动其中两条线段的位置，在原图中画出一个满足上题的直角三角形（顶点仍在格点，并标上必要的字母）．答：画出的直角三角形为△ ．
(3)、所画直角三角形的面积为 ．26. 如图，△ABC中，∠ACB=90°，AB=10cm，BC=6cm，若点P从点A出发，以每秒4cm的速度沿折线A-C-B-A运动，设运动时间为t秒（t＞0）．
(1)、若点P在AC上，且满足PA=PB时，求出此时t的值；(2)、若点P恰好在∠BAC的角平分线上，求t的值；(3)、在运动过程中，直接写出当t为何值时，△BCP为等腰三角形．