2018-2019学年初中数学浙教版九年级下册第一章 解直角三角形 单元测试卷B
试卷更新日期:2018-12-17 类型:单元试卷
一、选择题
-
1. 关于三角函数有如下公式:
sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ
cos(α+β)=cosαcosβ﹣sinαsinβ,cos(α﹣β)=cosαcosβ+sinαsinβ
tan(α+β)= (1﹣tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°cos60°+cos30°sin60°= =1
利用上述公式计算下列三角函数①sin105°= ,②tan105°=﹣2﹣ ,③sin15°= ,④cos90°=0
其中正确的个数有( )
A、1个 B、2个 C、3个 D、4个2. 在△ABC中,∠A,∠B均为锐角,且有|tanB﹣ |+(2cosA﹣1)2=0,则△ABC是( )A、直角(不等腰)三角形 B、等边三角形 C、等腰(不等边)三角形 D、等腰直角三角形3. tan35°•cotα=1,则α等于( )A、65° B、35° C、75° D、55°4. 如图,CD是平面镜,光线从A点出发经CD上点E反射照到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=12,则tanα值为( ) A、 B、 C、 D、5. 在△ABC中,∠C=90°,且两条直角边a,b满足a2﹣5ab+6b2=0,则tanA的值为( )A、5或6 B、2 C、3 D、2或36. 在Rt△ABC中,∠C=90°,若sinA= ,AB=2,则AC长是( )A、
A、 B、 C、 D、5. 在△ABC中,∠C=90°,且两条直角边a,b满足a2﹣5ab+6b2=0,则tanA的值为( )A、5或6 B、2 C、3 D、2或36. 在Rt△ABC中,∠C=90°,若sinA= ,AB=2,则AC长是( )A、 B、
C、
D、2
7. 如图,为了测量河对岸l1上两棵古树A,B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C,D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A,B之间的距离为( )
B、
C、
D、2
7. 如图,为了测量河对岸l1上两棵古树A,B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C,D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A,B之间的距离为( ) A、50m B、25m C、(50﹣
A、50m B、25m C、(50﹣ )m
D、(50﹣25 )m
8. “新中梁山隧道”于2017年11月21日开放通行,原中梁山隧道将封闭升级,扩容改造工程预计2018年3月全部完工,届时将实现双向8车道通行,隧道通行能力将增加一倍,沿线交通拥堵状况将有所缓解.图中线段AB表示该工程的部分隧道.无人勘测机从隧道侧的A点出发时,测得C点正上方的E点的仰角为45°,无人机飞行到E点后,沿着坡度i=1:3的路线EB飞行,飞行到D点正上方的F点时,测得A点的俯角为12°,其中EC=100米,A,B,C,D,E,F在同一平面内,则隧道AD段的长度约为( )米,(参考数据:tan12°≈0.2,cosl2°≈0.98)
)m
D、(50﹣25 )m
8. “新中梁山隧道”于2017年11月21日开放通行,原中梁山隧道将封闭升级,扩容改造工程预计2018年3月全部完工,届时将实现双向8车道通行,隧道通行能力将增加一倍,沿线交通拥堵状况将有所缓解.图中线段AB表示该工程的部分隧道.无人勘测机从隧道侧的A点出发时,测得C点正上方的E点的仰角为45°,无人机飞行到E点后,沿着坡度i=1:3的路线EB飞行,飞行到D点正上方的F点时,测得A点的俯角为12°,其中EC=100米,A,B,C,D,E,F在同一平面内,则隧道AD段的长度约为( )米,(参考数据:tan12°≈0.2,cosl2°≈0.98) A、200 B、250 C、300 D、5409. 如图,在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,DE⊥AC于点E,连接BE,则tan∠CBE的值等于( )
A、200 B、250 C、300 D、5409. 如图,在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,DE⊥AC于点E,连接BE,则tan∠CBE的值等于( ) A、 B、 C、
A、 B、 C、 D、
D、 10. 如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方向角为北偏东80°,测得C处的方向角为南偏东25°,航行1小时后到达C处,在C处测得A的方向角为北偏东20°,则C到A的距离是( )
10. 如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方向角为北偏东80°,测得C处的方向角为南偏东25°,航行1小时后到达C处,在C处测得A的方向角为北偏东20°,则C到A的距离是( ) A、15 km B、15 km C、15( + )km D、5( +3 )km
A、15 km B、15 km C、15( + )km D、5( +3 )km二、填空题
-
11. 如图,在Rt△ABC中,∠ACB=90°,CD是高,如果∠A=α,AC=4,那么BD= . (用锐角α的三角比表示)
 12. △ABC中,∠C=90°,tanA= ,则sinA+cosA= .13. 若∠α是锐角,且cosα=sin53°,则∠α的度数是 .14. 计算: = .15. 先用计算器求:tan20°≈ , tan40°≈ , tan60°≈ , tan80°≈ , 再按从小到大的顺序用“<”把tan20°,tan40°,tan60°,tan80°连接起来: . 归纳:正切值,角大值 .16. 如图,山坡的倾斜角∠ABC为30°,小明沿山坡BA从山脚B点步行到山顶A共走了100m,则山顶的高度AC是m.
12. △ABC中,∠C=90°,tanA= ,则sinA+cosA= .13. 若∠α是锐角,且cosα=sin53°,则∠α的度数是 .14. 计算: = .15. 先用计算器求:tan20°≈ , tan40°≈ , tan60°≈ , tan80°≈ , 再按从小到大的顺序用“<”把tan20°,tan40°,tan60°,tan80°连接起来: . 归纳:正切值,角大值 .16. 如图,山坡的倾斜角∠ABC为30°,小明沿山坡BA从山脚B点步行到山顶A共走了100m,则山顶的高度AC是m. 17. 某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°,则调整后楼梯AD的长为m.(结果保留根号)
17. 某处欲建一观景平台,如图所示,原设计平台的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°,则调整后楼梯AD的长为m.(结果保留根号)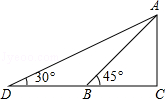 18. 如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为m.
18. 如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为m.
三、解答题
-
19. sin45°﹣cos45°+tan60°﹣30 .20. 【阅读学习】
刘老师提出这样一个问题:已知α为锐角,且tanα= ,求sin2α的值.
(1)、小娟是这样解决的:如图1,在⊙O中,AB是直径,点C在⊙O上,∠BAC=α,所以∠ACB=90°,tanα= = .
易得∠BOC=2α.设BC=x,则AC=3x,则AB= x.作CD⊥AB于D,求出CD=(用含x的式子表示),可求得sin2α= = .
(2)、【问题解决】已知,如图2,点M、N、P为圆O上的三点,且∠P=β,tanβ= ,求sin2β的值.
 21. 如图,在△ABC中,∠B=∠C=67.5°.
21. 如图,在△ABC中,∠B=∠C=67.5°. (1)、求sinA的值;(2)、求tanC的值.22. 如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
(1)、求sinA的值;(2)、求tanC的值.22. 如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)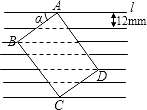 23. 如果等腰三角形两腰上的高之和等于底边上的高,请猜测这个三角形底角的正切值.24. 为了打通抚松到万良的最近公路,在一座小山的底部打通隧道.甲、乙两施工队按如图所示进行施工,甲施工队沿AC方向开山修路,乙施工队在这座小山的另一边E处沿射线CA方向同时施工.从AC上的一点B,取∠ABD=155°,经测得BD=1200m,∠D=65°,求开挖点E与点B之间的距离(结果精确到1m).【参考数据:sin65°=0.906,cos65°=0.423,tan65°=2.145.】
23. 如果等腰三角形两腰上的高之和等于底边上的高,请猜测这个三角形底角的正切值.24. 为了打通抚松到万良的最近公路,在一座小山的底部打通隧道.甲、乙两施工队按如图所示进行施工,甲施工队沿AC方向开山修路,乙施工队在这座小山的另一边E处沿射线CA方向同时施工.从AC上的一点B,取∠ABD=155°,经测得BD=1200m,∠D=65°,求开挖点E与点B之间的距离(结果精确到1m).【参考数据:sin65°=0.906,cos65°=0.423,tan65°=2.145.】 25. 如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的 长为12米,求大厅两层之间的距离BC的长.(结果精确到0.1米)(参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.60)
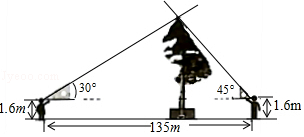
25. 如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的 长为12米,求大厅两层之间的距离BC的长.(结果精确到0.1米)(参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.60) 26. 清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”
26. 清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”小红和小阳进行了以下测量:如图所示,小红和小阳分别在树的东西两侧同一地平线上,他们用手平托三角板,保持三角板的一条直角边与地平面平行,然后前后移动各自位置,使目光沿着三角板的斜边正好经过树的最高点,这时,测得小红和小阳之间的距离为135米,他们的眼睛到地面的距离都是1.6米.通过计算说明小红和小阳谁的说法正确(计算结果精确到0.1)(参考数据 ≈1.41, ≈1.73, ≈2.24)