2018-2019学年数学八年级上册期末模拟试卷(浙江专版)
试卷更新日期:2018-12-16 类型:期末考试
一、选择题
-
1. 在以下永洁环保、绿色食品、节能、绿色环保四个标志中,是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 2. 如图,在△ABC中,∠B=60°,AB=AC,BC=3,则△ABC的周长为( )
2. 如图,在△ABC中,∠B=60°,AB=AC,BC=3,则△ABC的周长为( ) A、12 B、9 C、8 D、63. 若a <0,则点P(-a,2)应在( )
A、12 B、9 C、8 D、63. 若a <0,则点P(-a,2)应在( )
A、第一象限内 B、第二象限内 C、第三象限内 D、第四象限内4. 已知 a>b,则下列不等式中,正确的是( )A、-3a>-3b B、 C、a-3>b-3 D、3-a>3-b5. 如图,ΔABC中,AB=AC,∠BAC,∠ABC的角平分线相交于点D,若∠ADB= ,则∠BAC等于( ).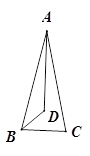 A、20° B、25° C、30° D、35°6. 如图,在△ABC中AB=AC,D,E两点分别在AC,BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )
A、20° B、25° C、30° D、35°6. 如图,在△ABC中AB=AC,D,E两点分别在AC,BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )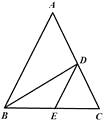 A、13cm B、11cm C、9cm D、7cm7. 下列命题中,逆命题不正确的是( )A、两直线平行,同旁内角互补 B、直角三角形的两个锐角互余 C、全等三角形对应角相等 D、直角三角形斜边上的中线等于斜边的一半8. 在平面直角坐标系中,点P在x轴的下方,y轴右侧,且到x轴的距离为5,到y轴距离为1,则点P的坐标为( )
A、13cm B、11cm C、9cm D、7cm7. 下列命题中,逆命题不正确的是( )A、两直线平行,同旁内角互补 B、直角三角形的两个锐角互余 C、全等三角形对应角相等 D、直角三角形斜边上的中线等于斜边的一半8. 在平面直角坐标系中,点P在x轴的下方,y轴右侧,且到x轴的距离为5,到y轴距离为1,则点P的坐标为( )
A、(1,-5) B、(5,1) C、(-1,5) D、(5,-1)9. 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )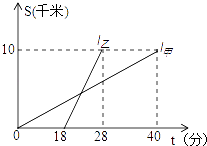 A、4个 B、3个 C、2个 D、1个10. 设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )
A、4个 B、3个 C、2个 D、1个10. 设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )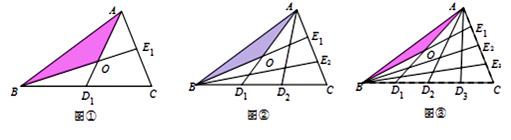 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 命题“如果两个角都是直角,那么这两个角相等”的逆命题.
12. 新定义:[a,b,c]为函数y= (a,b,c为实数)的“关联数”.若“关联数”为 [m-2,m,1]的函数为一次函数,则m的值为 .13. 若周长为1的四边形的四条边的长为a、b、c、d且a≥b≥c≥d,则a的取值范围是 .
14. 如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD= .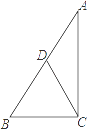 15. 如图为 6 个边长相等的正方形的组合图形,则∠1+∠2+∠3=°
15. 如图为 6 个边长相等的正方形的组合图形,则∠1+∠2+∠3=°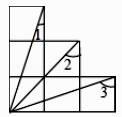 16. 如图已知正方形ABCD的对角线长为 ,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长。
16. 如图已知正方形ABCD的对角线长为 ,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长。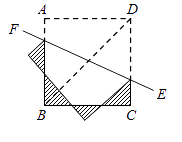
三、解答题
-
17. 已知:如图,OF是∠AOC和∠BOD的平分线,OA=OC,OB=OD.
求证:AB=CD.
 18. 如图,在方格纸中,点A,D都在格点上,作三角形ABC,使其满足下列条件.(点B,C不与点D重合)
18. 如图,在方格纸中,点A,D都在格点上,作三角形ABC,使其满足下列条件.(点B,C不与点D重合)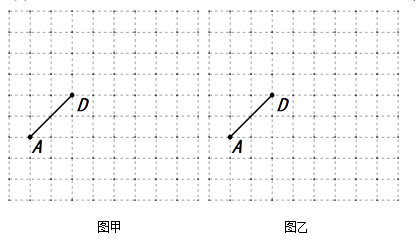 (1)、在图甲中,作格点等腰△ABC,使AD为△ABC的高线.
(1)、在图甲中,作格点等腰△ABC,使AD为△ABC的高线.
(2)、在图乙中,作格点钝角△ABC,使AD为△ABC的角平分线
19. 深化理解:新定义:对非负实数x“四舍五入”到个位的值记为<x>,
即:当n为非负整数时,如果n﹣ ≤x<n+ ,则<x>=n;
反之,当n为非负整数时,如果<x>=n,则n﹣ ≤x<n+ .
例如:<0>=<0.48>=0,<0.64>=<1.49>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)、填空:①<π>=(π为圆周率); ②如果<x﹣1>=3,则实数x的取值范围为 .(2)、若关于x的不等式组 的整数解恰有3个,求a的取值范围.(3)、求满足<x>= x 的所有非负实数x的值.20. 端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中休息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程 , 与时间 之间的函数关系的图象 请根据图象提供的信息,解决下列问题: (1)、图中E点的坐标是 , 题中 ,甲在途中休息h;(2)、求线段CD的解析式,并写出自变量x的取值范围;(3)、两人第二次相遇后,又经过多长时间两人相距20km?21. 某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22 400万元,但不超过22 500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
(1)、图中E点的坐标是 , 题中 ,甲在途中休息h;(2)、求线段CD的解析式,并写出自变量x的取值范围;(3)、两人第二次相遇后,又经过多长时间两人相距20km?21. 某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22 400万元,但不超过22 500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:型号
A
B
成本(万元/台)
200
240
售价(万元/台)
250
300
(1)、该厂对这两型挖掘机有哪几种生产方案?
(2)、该厂如何生产能获得最大利润?(3)、根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产获得最大利润?(注:利润=售价﹣成本)22. 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.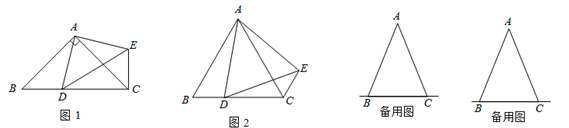 (1)、如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)、设 , .
(1)、如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)、设 , .①如图2,当点在线段BC上移动,则 , 之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则 , 之间有怎样的数量关系?请直接写出你的结论.
23. 如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a,b满足|a﹣4|+ =0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.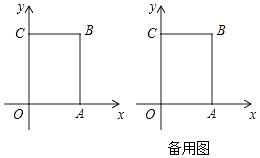 (1)、点B的坐标为 , 当点P移动3.5秒时,点P的坐标;(2)、在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间;
(1)、点B的坐标为 , 当点P移动3.5秒时,点P的坐标;(2)、在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间;
(3)、在移动过程中,当△OBP的面积是10时,求点P移动的时间.