2018-2019学年九年级数学上册期末检测卷(深圳专版)
试卷更新日期:2018-12-14 类型:期末考试
一、选择题
-
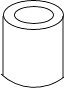
1. 2cos45°的值等于( )A、 B、 C、 D、22. 某种零件模型可以看成如图所示的几何体(空心圆柱),该几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 二次函数y=-3(x+1)2-2的顶点坐标是( )
3. 二次函数y=-3(x+1)2-2的顶点坐标是( )
A、(-1,-2) B、(-1,2) C、(1,-2) D、(1,2)4. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( ) A、 B、 C、 D、5. 某校安排三辆车,组织九年级学生团员去敬老院参加学雷锋活动,其中小王与小菲都可以从这三辆车中任选一辆搭乘,则小王与小菲同车的概率为( )A、 B、 C、 D、6. 下列性质中,正方形具有而菱形不一定具有的性质是( )A、四条边相等 B、对角线互相平分 C、对角线相等 D、对角线互相垂直7. 如图,在▱ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )
A、 B、 C、 D、5. 某校安排三辆车,组织九年级学生团员去敬老院参加学雷锋活动,其中小王与小菲都可以从这三辆车中任选一辆搭乘,则小王与小菲同车的概率为( )A、 B、 C、 D、6. 下列性质中,正方形具有而菱形不一定具有的性质是( )A、四条边相等 B、对角线互相平分 C、对角线相等 D、对角线互相垂直7. 如图,在▱ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )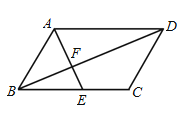 A、S△ADF=2S△BEF B、BF=DF C、四边形AECD是等腰梯形 D、∠AEB=∠ADC8. 某市商品房的均价原为18150元/m2 , 经过连续两次降价后均价为15000元/m2 . 设平均每次降价的百分率为x,根据题意所列方程正确的是( )A、18150(1﹣x)2=18150﹣15000 B、18150(1﹣x2)=15000 C、18150(1﹣2x)=15000 D、18150(1﹣x)2=150009. 关于二次函数y=2x2+3,下列说法中正确的是( )A、它的开口方向是向下 B、当x<﹣1时,y随x的增大而减小 C、它的顶点坐标是(2,3) D、当x=0时,y有最大值是310. 一个三角形的两边长分别为3和6,第三边的边长是方程(x﹣2)(x﹣4)=0的根,则这个三角形的周长是( )A、11 B、11或13 C、13 D、以上选项都不正确11. 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上,反比例函数y= (x>0)的图象经过顶点B,则k的值为( )
A、S△ADF=2S△BEF B、BF=DF C、四边形AECD是等腰梯形 D、∠AEB=∠ADC8. 某市商品房的均价原为18150元/m2 , 经过连续两次降价后均价为15000元/m2 . 设平均每次降价的百分率为x,根据题意所列方程正确的是( )A、18150(1﹣x)2=18150﹣15000 B、18150(1﹣x2)=15000 C、18150(1﹣2x)=15000 D、18150(1﹣x)2=150009. 关于二次函数y=2x2+3,下列说法中正确的是( )A、它的开口方向是向下 B、当x<﹣1时,y随x的增大而减小 C、它的顶点坐标是(2,3) D、当x=0时,y有最大值是310. 一个三角形的两边长分别为3和6,第三边的边长是方程(x﹣2)(x﹣4)=0的根,则这个三角形的周长是( )A、11 B、11或13 C、13 D、以上选项都不正确11. 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上,反比例函数y= (x>0)的图象经过顶点B,则k的值为( )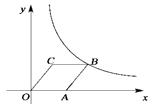 A、12 B、20 C、24 D、3212. 已知二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象大致是( )
A、12 B、20 C、24 D、3212. 已知二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象大致是( )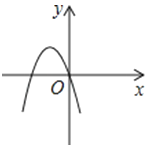 A、
A、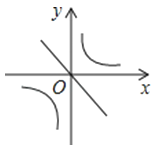 B、
B、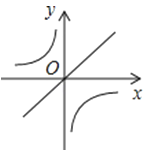 C、
C、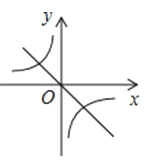 D、
D、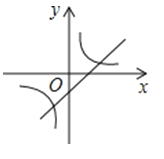
二、填空题
-
13. 若3是关于x的方程x2﹣x+c=0的一个根,则方程的另一个根等于 .14. 为了估算湖里有多少条鱼,从湖里捕上100条做上标记,然后放回湖里,经过一段时间待标记的鱼全混合于鱼群中后,第二次捕得200条,发现其中带标记的鱼25条,我们可以估算湖里有鱼条.15. 如图,四边形ABCD中,对角线AC⊥BD,E、F、G、H分别是各边的中点,若AC=8,BD=6,则四边形EFGH的面积是 .
 16. 如图,已知双曲线 y=(k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=4,则k= .
16. 如图,已知双曲线 y=(k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=4,则k= .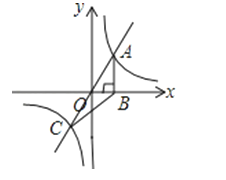
三、解答题
-
17. 解方程:x2﹣6x﹣1=0.18. 计算: +(﹣ )﹣1+|1﹣ |﹣4sin45°.19. 一个口袋中有1个黑球和若干个白球,这些球除颜色外其他都相同.已知从中任意摸取一个球,摸得黑球的概率为 .
(1)求口袋中白球的个数;
(2)如果先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.用列表法或画树状图法加以说明.
20. 如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据: , )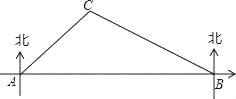 21.
21.如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
 22. 某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
22. 某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.①写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式,并写出x的取值范围.
②若商场要每天获得销售利润2000元,销售单价应定为多少元?
③求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?
23. 如图所示,在平面直角坐标系中,Rt△OBC的两条直角边分别落在x轴、y轴上,且OB=1,OC=3,将△OBC绕原点O顺时针旋转90°得到△OAE,将△OBC沿y轴翻折得到△ODC,AE与CD交于点F.
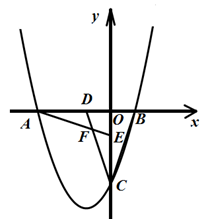
(1)若抛物线过点A、B、C, 求此抛物线的解析式;
(2)求△OAE与△ODC重叠的部分四边形ODFE的面积;
(3)点M是第三象限内抛物线上的一动点,点M在何处时△AMC的面积最大?最大面积是多少?求出此时点M的坐标.