广东省佛山市禅城区2018-2019学年高三理数统一调研考试试卷(二)
试卷更新日期:2018-11-30 类型:高考模拟
一、单选题
-
1. 已知复数 ,则复数z的虚部为( )A、
 B、
B、 C、
C、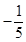 D、
D、 2. 已知集合 , ,则 ( )A、
2. 已知集合 , ,则 ( )A、 B、
B、 C、
C、 D、
D、 3. 公差不为0的等差数列 的前n项和为 ,若 ,且 ,则 的值为( )A、15 B、25 C、13 D、234. 已知命题p:命题“ ”的否定是“ ”;命题q:在△ABC中角A、B、C的对边分别为a、b、c,则“ ”是“a>b”的充要条件,则下列命题为真命题的是( )A、
3. 公差不为0的等差数列 的前n项和为 ,若 ,且 ,则 的值为( )A、15 B、25 C、13 D、234. 已知命题p:命题“ ”的否定是“ ”;命题q:在△ABC中角A、B、C的对边分别为a、b、c,则“ ”是“a>b”的充要条件,则下列命题为真命题的是( )A、 B、
B、 C、
C、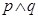 D、
D、 5. 已知函数 (其中 为自然对数的底数),则 的大致图象为( )A、
5. 已知函数 (其中 为自然对数的底数),则 的大致图象为( )A、 B、
B、 C、
C、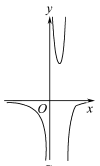 D、
D、 6. 下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为y=0.8x-155,后因某未知原因第五组数据的y值模糊不清,此位置数据记为m(如下所示),则利用回归方程可求得实数m的值为( )
6. 下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为y=0.8x-155,后因某未知原因第五组数据的y值模糊不清,此位置数据记为m(如下所示),则利用回归方程可求得实数m的值为( )x
196
197
200
203
204
y
1
3
6
7
m
A、8.3 B、8 C、8.1 D、8.27. 如图所示的阴影部分是由 轴及曲线 围成,在矩形区域 内随机取一点,则该点取自阴影部分的概率是( )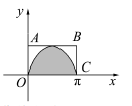 A、
A、 B、
C、
B、
C、 D、
D、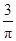 8. 已知 ,则 ( )A、
8. 已知 ,则 ( )A、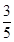 B、
B、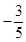 C、
C、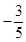 或1
D、1
9. 定义运算: ,将函数 ( )的图像向左平移 个单位所得图像对应的函数为偶函数,则 的最小值是( )A、
或1
D、1
9. 定义运算: ,将函数 ( )的图像向左平移 个单位所得图像对应的函数为偶函数,则 的最小值是( )A、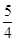 B、
C、
D、
10. 设x,y满足约束条件 ,若目标函数 仅在点(1,0)处取得最小值,则a的取值范围( )A、(-6,-3) B、(-6,3) C、(0,3) D、(-6,0]11. 若函数 在区间 上为减函数,则a的取值范围是( )A、
B、
C、
D、
10. 设x,y满足约束条件 ,若目标函数 仅在点(1,0)处取得最小值,则a的取值范围( )A、(-6,-3) B、(-6,3) C、(0,3) D、(-6,0]11. 若函数 在区间 上为减函数,则a的取值范围是( )A、 B、
B、 C、
C、 D、(1,2]
12. 若关于x的方程 有三个不相等的实数解 ,且 ,其中m∈R,e为自然对数的底数,则 的值为( )A、1+m B、e C、m-1 D、1
D、(1,2]
12. 若关于x的方程 有三个不相等的实数解 ,且 ,其中m∈R,e为自然对数的底数,则 的值为( )A、1+m B、e C、m-1 D、1二、填空题
-
13. 等边△ABC中,边长为2,则 =14. 若函数 为偶函数,则 =15. 定义在R上的可导函数 ,当 时, 恒成立, , ,则a,b,c的大小关系为
三、解答题
-
16. 已知在平面直角坐标系xOy中,直线 的参数方程为 (t为参数),曲线 的方程为 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.(1)、求直线 和曲线C1的极坐标系方程;(2)、曲线C2: 分别交直线 和曲线C1交于A、B,求 的最大值.17. 已知 是定义在(-1,1)上的奇函数,当x∈(0,1)时, .(1)、求 在(-1,1)上的解析式;(2)、若 是周期为2的函数,且x∈(-1,1)时 ,求 时的解析式.18. △ABC的对边分别为a,b,c,满足 .(1)、求角B;(2)、若 ,试求 的值.19. 已知数列 的前n项和为 , ,且(1)、求数列 的通项公式;(2)、设 ,求 的前n项和 .20. 一项研究机构培育一种新型水稻品种,首批培育幼苗2000株,株长均介于185mm-235mm,从中随机抽取100株对株长进行统计分析,得到如下频率分布直方图
附: ;若X: ,则 ;
;
 (1)、求样本平均株长 和样本方差 (同一组数据用该区间的中点值代替);(2)、假设幼苗的株长X服从正态分布 N , 其中 近似为样本平均数 , 近似为样本方差 ,试估计2000株幼苗的株长位于区间(201,219)的株数;
(1)、求样本平均株长 和样本方差 (同一组数据用该区间的中点值代替);(2)、假设幼苗的株长X服从正态分布 N , 其中 近似为样本平均数 , 近似为样本方差 ,试估计2000株幼苗的株长位于区间(201,219)的株数;
(3)、在第(2)问的条件下,选取株长在区间(201,219)内的幼苗进入育种试验阶段,若每株幼苗开花的概率为 ,开花后结穗的概率为 ,设最终结穗的幼苗株数为 ,求 的数学期望.21. 已知函数 .(1)、求函数 的单调区间;(2)、若函数 有两个零点 ,证明 .