浙江省慈溪市六校2018-2019学年高一上学期数学期中考试试卷
试卷更新日期:2018-11-30 类型:期中考试
一、单选题
-
1. 已知集合 , ,则 ( )A、
 B、
B、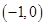 C、
C、 D、
D、 2. 下列函数中,既是奇函数,又在 上为增函数的是( )A、
2. 下列函数中,既是奇函数,又在 上为增函数的是( )A、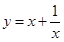 B、
B、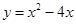 C、
C、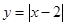 D、
D、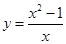 3. 下列各组函数f(x)与g(x)的图象相同的是( )A、
3. 下列各组函数f(x)与g(x)的图象相同的是( )A、 B、
B、 C、
C、 D、
D、 4. 函数 的单调递减区间是( )A、
4. 函数 的单调递减区间是( )A、 B、
B、 C、
C、 D、
D、 5. 若 ,则 , , , 的大小关系为( )A、
5. 若 ,则 , , , 的大小关系为( )A、 B、
B、 C、
C、 D、
D、 6. 若直角坐标平面内A、B两点满足:①点A、B都在函数f(x)的图象上;②点A、B关于原点对称,则称点(A , B)是函数f(x)的一个“姊妹点对”.点对(A , B)与(B , A)可看作是同一个“姊妹点对”,已知函数 ,则f(x)的“姊妹点对”有( )A、0个 B、1个 C、2个 D、3个7. 已知函数 当 时, ,则 的取值范围是( )A、
6. 若直角坐标平面内A、B两点满足:①点A、B都在函数f(x)的图象上;②点A、B关于原点对称,则称点(A , B)是函数f(x)的一个“姊妹点对”.点对(A , B)与(B , A)可看作是同一个“姊妹点对”,已知函数 ,则f(x)的“姊妹点对”有( )A、0个 B、1个 C、2个 D、3个7. 已知函数 当 时, ,则 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 8. 已知对数函数f(x)=logax是增函数,则函数f(|x|+1)的图象大致是( )A、
8. 已知对数函数f(x)=logax是增函数,则函数f(|x|+1)的图象大致是( )A、 B、
B、 C、
C、 D、
D、 9. 已知 是定义域为 的奇函数,满足 .若 ,则 ( )A、-2018 B、0 C、2 D、5010. 已知函数 ,给出下列命题:① 必是偶函数;②当 时, 的图像关于直线 对称;③若 ,则 在区间 上是增函数;④若 ,在区间 上 有最大值 . 其中正确的命题序号是:( )A、③ B、②③ C、③④ D、①②③
9. 已知 是定义域为 的奇函数,满足 .若 ,则 ( )A、-2018 B、0 C、2 D、5010. 已知函数 ,给出下列命题:① 必是偶函数;②当 时, 的图像关于直线 对称;③若 ,则 在区间 上是增函数;④若 ,在区间 上 有最大值 . 其中正确的命题序号是:( )A、③ B、②③ C、③④ D、①②③二、填空题
-
11. 设函数 ,则 , 方程 的解为 .
12. 已知 ,若 , ,则 = , =.13. ①函数 的图象必过定点,定点坐标为 .②已知函数y=f(x2-1)的定义域为[- , ],则函数y=f(x)的定义域为 .
14. 若指数函数 的图像过点 ,则 ;不等式 的解集为 .15. 设任意实数 ,要使 恒成立,则 的最小值为 .16. 定义在 上的偶函数 在 上是增函数,且 ,则使得不等式 成立 的取值范围是.17. 定义区间 的长度 均为 ,多个互无交集的区间的并集长度为各区间长度之和,例如 的长度 。用 表示不超过 的最大整数,例如 。记 。设 , ,若用 、 和 分别表示不等式 、方程 和不等式 解集区间的长度,则当 时, .三、解答题
-
18.(1)、(2)、已知 ,求 和 的值.19. 已知集合 , .(1)、分别求 , ;(2)、已知集合 ,若 ,求实数 的取值范围.