2018-2019学年数学浙教版九年级上册第4章 相似三角形 单元检测b卷
试卷更新日期：2018-09-14 类型：单元试卷
一、选择题
-
1. 某校每位学生上、下学期各选择一个社团，下表为该校学生上、下学期各社团的人数比例．若该校上、下学期的学生人数不变，相较于上学期，下学期各社团的学生人数变化，下列叙述何者正确？（ ）
舞蹈社
溜冰社
魔术社
上学期
3
4
5
下学期
4
3
2
A、舞蹈社不变，溜冰社减少 B、舞蹈社不变，溜冰社不变 C、舞蹈社增加，溜冰社减少 D、舞蹈社增加，溜冰社不变2. 如图，正方形ABCD中，点E在边BC上，且CE=2BE．连接BD、DE、AE，且AE交BD于F，OG为△BDE的中位线．下列结论：①OG⊥CD；②AB=5OG；③ ；④BF=OF；⑤ ，其中正确结论的个数是（ ）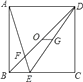
A、2 B、3 C、4 D、53. 如图，在△ABC中，D为AB边上一点，E为CD中点，AC= ，∠ABC=30°，∠A=∠BED=45°，则BD的长为（ ）
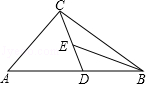A、
B、 +1﹣
C、 ﹣
D、 ﹣1
4. 如图，已知点D、F在△ABC的边AB上，点E在边AC上，且DE∥BC，要使得EF∥CD，还需添加一个条件，这个条件可以是（ ）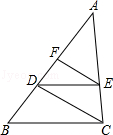
A、
B、
C、
D、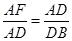
5. 兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0.4米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.4米，则树高为（ ）
A、11.5米 B、11.75米 C、11.8米 D、12.25米6. 如图，将一张直角三角形纸片沿虚线剪成甲、乙、丙三块，其中甲、丙为梯形，乙为三角形．根据图中标示的边长数据，比较甲、乙、丙的面积大小，下列判断何者正确？（ ）
A、甲＞乙，乙＞丙 B、甲＞乙，乙＜丙 C、甲＜乙，乙＞丙 D、甲＜乙，乙＜丙7.如图所示，点A，B，C，D，E，F，G，H，K都是8×8方格纸中的格点，为使△DEM∽△ABC，则点M应是F、G、H、K四点中的（ ）
A、F B、G C、H D、K8. 如图，正方形ABCD中，P为对角线上的点，PB=AB，连PC，作CE⊥CP交AP的延长线于E，AE交CD于F，交BC的延长线于G，则下列结论：①E为FG的中点；②FG2=4CF•CD；③AD=DE；④CF=2DF．其中正确的个数是（ ）
A、1个 B、2个 C、3个 D、4个9. 如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论中正确的个数有（ ）①∠EAF=45°；②△ABE∽△ACD；③AE平分∠CAF；④BE2+DC2=DE2 ．
A、1个 B、2个 C、3个 D、4个10. 如图，菱形ABCD中，AB=AC，点E，F在AB，BC上，AE=BF，AF，CE交于G，GD和AC交于H，则下列结论中成立的有（ ）个．①△ABF≌△CAE；②∠AGC=120°；③DG=AG+GC；④AD2=DH•DG；⑤△ABF≌△DAH．
A、2 B、3 C、4 D、5二、填空题
-
11. 如图，在△ABC中，D，E两点分别在边BC，AB上，DE∥AC，过点E作EF∥DC，交∠ACB的平分线于点F，连结DF，若∠EDF=∠B，且BC=4，BD=1，那么EF的长度是 ．
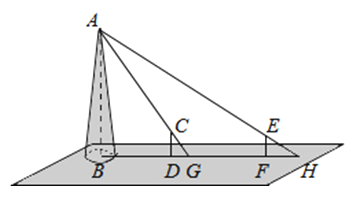
12. 在Rt△ABC中，C为直角顶点，过点C作AB的垂线，若D为垂足，若AC、BC为方程x2﹣6x+2=0的两根，则AD•BD的值等于13.如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，则建筑物的高是 米．
14. 如图，正方形ABCD的边长为1，动点E在BC上，∠AEF=90°，EF交DC于F，当线段FC最长时，BE的长为 ．
15. 如图，在平面直角坐标系中，△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形，且点B（3，1），B′（6，2）．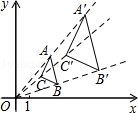
①若点A（ ，3），则A′的坐标为；
②△ABC与△A′B′C′的相似比等于；
③若△ABC的面积为m，则△A′B′C′的面积= ．
16. 如图，在△ABC中，AB=AC，点D、E分别在边BC、AB上，且∠ADE=∠B，如果DE：AD=2：5，BD=3，那么AC= ．
17. 在平面直角坐标系中，第1个正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1 ， 作第2个正方形A1B1C1C；延长C1B1交x轴于点A2 ， 作第3个正方形A2B2C2C1…按这样的规律进行下去，第2个正方形的面积为；第2011个正方形的面积为 ．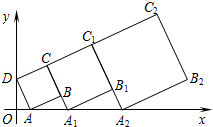
18. 如图，在直角梯形ABCD中，AD∥BC，∠B=90°，E为AB上一点，且ED平分∠ADC，EC平分∠BCD，则下列结论：①DE⊥EC；②点E是AB中点；③AD•BC=BE•DE；④CD=AD+BC．其中正确的有 ．
三、解答题
-
19. 如图1，△ABC中，点D在线段AB上，点E在线段CB延长线上，且BE=CD，EP∥AC交直线CD于点P，交直线AB于点F，∠ADP=∠ACB．
(1)、图1中是否存在与AC相等的线段？若存在，请找出，并加以证明，若不存在，说明理由；(2)、若将“点D在线段AB上，点E在线段CB延长线上”改为“点D在线段BA延长线上，点E在线段BC延长线上”，其他条件不变（如图2）．当∠ABC=90°，∠BAC=60°，AB=2时，求线段PE的长．20. 一块直角三角形木板，它的一条直角边AB长1.5m，面积为1.5m2 ． 甲、乙两位木匠分别按图①、②把它加工成一个正方形桌面．请说明哪个正方形面积较大（加工损耗不计）．
21. 如图，在△ABC中，AC=BC，∠ACB=90°，CD⊥AB，垂足为D，点E在AC上，BE交CD于点G，EF⊥BE交AB于点F，
(1)、如图1：若EA=CE，探索线段EF与EG的数量关系，并证明你的结论；(2)、如图2：若EA=2CE，探索线段EF与EG的数量关系，并证明你的结论；(3)、若EA=kCE，探索线段EF与EG的数量关系，请直接写出你的结论．22. 如图，在直角梯形OABC中，OA∥BC，A、B两点的坐标分别为A（13，0），B（11，12）．动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿x轴向终点A运动，点Q以每秒1个单位的速度沿BC方向运动；当点P停止运动时，点Q也同时停止运动．线段PQ和OB相交于点D，过点D作DE∥x轴，交AB于点E，射线QE交x轴于点F．设动点P、Q运动时间为t（单位：秒）．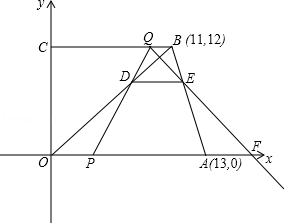
(1)、当t为何值时，四边形PABQ是平行四边形．(2)、△PQF的面积是否发生变化？若变化，请求出△PQF的面积s关于时间t的函数关系式；若不变，请求出△PQF的面积．(3)、随着P、Q两点的运动，△PQF的形状也随之发生了变化，试问何时会出现等腰△PQF？23. 如图，等腰梯形ABCD中，AB=CD，AD=2，BC=4．点M从B点出发以每秒2个单位的速度向终点C运动；同时点N从D点出发以每秒1个单位的速度向终点A运动．过点N作NP⊥BC，垂足为P，NP=2．连接AC交NP于Q，连接MQ．若点N运动时间为t秒
(1)、请用含t的代数式表示PC；(2)、求△CMQ的面积S与时间t的函数关系式，当t取何值时，S有最大值？最大值是多少？24. 如图，在矩形ABCD中，E为AB边上一点，EC平分∠DEB，F为CE的中点，连接AF，BF，过点E作EH∥BC分别交AF，CD于G，H两点．
(1)、求证：DE=DC；(2)、求证：AF⊥BF；(3)、当AF•GF=28时，请直接写出CE的长．25. 本题为选做题，从甲、乙两题中选做一题即可，如果两题都做，只以甲题计分．(1)、甲题：关于x的一元二次方程x2+（2k﹣3）x+k2=0有两个不相等的实数根α、β．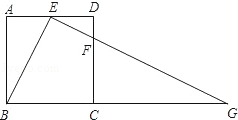
①求k的取值范围；
②若α+β+αβ=6，求（α﹣β）2+3αβ﹣5的值．
(2)、乙题：如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF= DC，连接EF并延长交BC的延长线于点G①求证：△ABE∽△DEF；
②若正方形的边长为4，求BG的长．