浙江省温州市龙港地区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2018-11-30 类型：期中考试
一、单选题
-
1. 在一些美术字中，有些是轴对称图形.下列汉字字体中，可以看作轴对称图形的是（ ）A、最 B、美 C、温 D、州2. 已知△ABC的两个内角∠A=30°，∠B=70°，则△ABC是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形3. 在△ABC中，∠A是钝角，下列图中画BC边上的高线正确的是（ ）A、
B、
C、
D、
4. 下列长度的三条线段能组成三角形的是（ ）A、1，2，3 B、3，8，4 C、6，4，5 D、5，2，85. 如图，在△ABC中，∠B=65°，∠DCA=100°，则∠A的度数是（ ）
A、55° B、45° C、35° D、25°6. 等腰三角形的边长是3和8，则它的周长是（ ）
A、11 B、14 C、19 D、14或197. 下列选项中，可以用来证明命题“若 ，则 ”是假命题的反例的是（ ）A、a=－1 B、a=0 C、a=1 D、a=28. 在 中，∠ACB=90°，斜边 的中垂线 分别交BC，AB于点D，E．已知BD=5，CD=3，则AC的长为（ ）
A、8 B、4 C、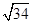
D、2
9. 如图，在△ABC中，∠C=29°，D为边AC上一点，且AB=AD，DB=DC，则∠A的度数为（ ）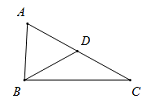
A、54° B、58° C、61° D、64°10. 如图，△ABC与△CED均为等边三角形，且B，C，D三点共线．线段BE，AD相交于点O，AF⊥BE于点F．若OF=1，则AF的长为（ ）
A、1 B、
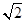C、
D、2
二、填空题
-
11. 若等边三角形的一边长为4厘米，则它的周长为厘米．12. 如图，已知∠ACB=∠DBC，请添加一个条件 ， 使得△ABC≌△DCB．
13. 命题“在同一个三角形中，等角对等边”的逆命题是 ．14. 如图，BD是Rt△ABC斜边AC上的中线，若∠CDB=130°，则∠C=度．
15. 如图，在△ABC中，∠C=90°，BD平分∠ABC，交AC于点D．若DC=4，则点D到AB的距离为 ．
16. 一个等腰三角形的底边长为5，一腰上的中线把它的周长分成的两部分的差为2，则这个等腰三角形的腰长为 ．17. 如图，已知∠A=90°，AC=AB=4，CD=2，BD=6．则∠ACD=度．
18. 如图，∠ABC=30°，AB=8，F是射线BC上一动点，D在线段AF上，以AD为腰作等腰直角三角形ADE（点A，D，E以逆时针方向排列），且AD=DE=1，连结EF，则EF的最小值为 ．
三、解答题
-
19. 如图，已知△ABC，按下列要求作图（第（1）、（2）小题用尺规作图，
第（3）小题不限作图工具，保留作图痕迹）．
①作∠B的角平分线；
②作BC的中垂线；
③以BC边所在直线为对称轴，作△ABC的轴对称图形．
20. 如图，∠ABE=∠ACD=90°，AE=AD，∠ABC=∠ACB．求证：∠BAE=∠CAD．
请补全证明过程，并在括号里写上理由．
证明：在△ABC中，
∵∠ABC=∠ACB
∴AB=（）
在Rt△ABE和Rt△ACD中，
∵=AC，=AD
∴Rt△ABE≌Rt△ACD（）
∴∠BAE=∠CAD（ ）
21. 如图，点B，F，C，E在同一直线上，且∠A=∠D，AB=DE，∠B=∠E．求证：BF=CE．
22. 如图，∠BAD=∠CAE，AB=AD，AC=AE．且E，F，C，D在同一直线上．
(1)、求证：△ABC≌△ADE；(2)、若∠B=30°，∠BAC=100°，点F是CE的中点，连结AF，求∠FAE的度数．
