浙江省绍兴市柯桥区六校联盟2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2018-11-30 类型:期中考试
一、单选题
-
1. 下列图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 三角形两边长为2,5,则第三边的长不能是( )A、4 B、5 C、6 D、73. 不等式1﹣x≥2的解在数轴上表示正确的是( )A、
2. 三角形两边长为2,5,则第三边的长不能是( )A、4 B、5 C、6 D、73. 不等式1﹣x≥2的解在数轴上表示正确的是( )A、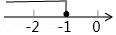 B、
B、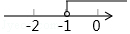 C、
C、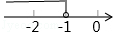 D、
D、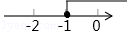 4. 如图,能用AAS来判定△ACD≌△ABE需要添加的条件是( )
4. 如图,能用AAS来判定△ACD≌△ABE需要添加的条件是( )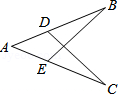 A、∠AEB=∠ADC,BE=CD B、AC=AB,∠B=∠C C、AC=AB,AD=AE D、∠AEB=∠ADC,∠B=∠C5. 在Rt△ABC中,∠C=90°,∠A﹣∠B=70°,则∠A的度数为( )A、80° B、70° C、60° D、50°6. 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.则下列四种不同方法的作图中正确的是( )
A、∠AEB=∠ADC,BE=CD B、AC=AB,∠B=∠C C、AC=AB,AD=AE D、∠AEB=∠ADC,∠B=∠C5. 在Rt△ABC中,∠C=90°,∠A﹣∠B=70°,则∠A的度数为( )A、80° B、70° C、60° D、50°6. 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC.则下列四种不同方法的作图中正确的是( ) A、
A、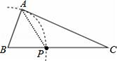 B、
B、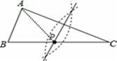 C、
C、 D、
D、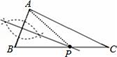 7. 若x+5>0,则( )A、x+2>0 B、x﹣1<0 C、﹣2x<14 D、
7. 若x+5>0,则( )A、x+2>0 B、x﹣1<0 C、﹣2x<14 D、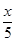 <﹣1
8. 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )
<﹣1
8. 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )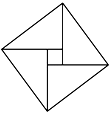 A、4 B、6 C、8 D、109. 如图,∠AOB=45°,点M,N在边OA上,OM=2,ON=4,点P是边OB上的点,则能使点P,M,N构成等腰三角形的点P的个数有( )
A、4 B、6 C、8 D、109. 如图,∠AOB=45°,点M,N在边OA上,OM=2,ON=4,点P是边OB上的点,则能使点P,M,N构成等腰三角形的点P的个数有( )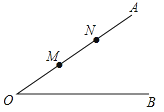 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 在Rt△ABC中,锐角∠A=25°,则另一个锐角∠B= .11. 如图,CD是Rt△ABC斜边AB上的高,将△ACD沿CD折叠,A点恰好落在AB的中点E处,则∠B等于度.
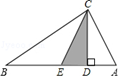 12. 如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BOC=°.
12. 如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BOC=°.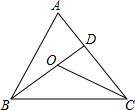 13. 一次知识竞赛共有22道题,答对一题的5分,不答题得0分,答错一题扣2分,小明有两题没答,成绩超过75分,则小明至多答错了道题.14. △ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE,若∠A=30°,AB=AC,则∠BDE= .
13. 一次知识竞赛共有22道题,答对一题的5分,不答题得0分,答错一题扣2分,小明有两题没答,成绩超过75分,则小明至多答错了道题.14. △ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE,若∠A=30°,AB=AC,则∠BDE= . 15. 如图,△ABC中,AB=AC,∠A=40°,BD=CF,BE=CD,则∠EDF的度数为 .
15. 如图,△ABC中,AB=AC,∠A=40°,BD=CF,BE=CD,则∠EDF的度数为 . 16. 如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=42°,则∠AEB= .
16. 如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=42°,则∠AEB= .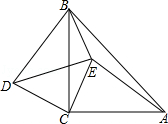 17. 如图有一张简易的活动小餐桌,现测得OA=OB=30cm,OC=OD=50cm,桌面离地面的高度为40cm,则两条桌腿的张角∠COD的度数为度.
17. 如图有一张简易的活动小餐桌,现测得OA=OB=30cm,OC=OD=50cm,桌面离地面的高度为40cm,则两条桌腿的张角∠COD的度数为度.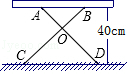 18. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .19. 如图,等边△ABC中,BD=CE,AD与BE交于P,AQ⊥BE,垂足为Q,PD=2,PQ=6,则BE的长为 .
18. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .19. 如图,等边△ABC中,BD=CE,AD与BE交于P,AQ⊥BE,垂足为Q,PD=2,PQ=6,则BE的长为 .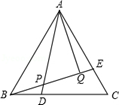
三、解答题
-
20. 解不等式 ≤ ,并把解表达在数轴上.
 21. 图( )和图( )是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的长均为1,请分别画出符合要求的图形,所画图形的各顶点必须与方格纸中的小正方形的顶角重合.
21. 图( )和图( )是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的长均为1,请分别画出符合要求的图形,所画图形的各顶点必须与方格纸中的小正方形的顶角重合.
 (1)、请在图( )中画出一个面积为6的等腰三角形.(2)、请在图( )中画出一个边长为 的等腰直角三角形.22. 为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B 两种型号家用净水器160台,A型号家用净水器进价是1500元/台,售价2100元/台,B型号家用净水器进价是3500元/台,售价是4300元/台.为保证售完这160台家用净水器的毛利润不低于116000元,求A型号家用净水器最多能购进多少台?(注:毛利润=售价-进价)23. 如图,已知AD为△ABC的中线,延长AD,分别过点B,C作BE⊥AD,CF⊥AD.
(1)、请在图( )中画出一个面积为6的等腰三角形.(2)、请在图( )中画出一个边长为 的等腰直角三角形.22. 为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B 两种型号家用净水器160台,A型号家用净水器进价是1500元/台,售价2100元/台,B型号家用净水器进价是3500元/台,售价是4300元/台.为保证售完这160台家用净水器的毛利润不低于116000元,求A型号家用净水器最多能购进多少台?(注:毛利润=售价-进价)23. 如图,已知AD为△ABC的中线,延长AD,分别过点B,C作BE⊥AD,CF⊥AD.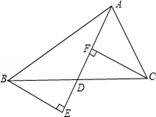 (1)、求证:△BED≌△CFD.(2)、若∠EAC=45°,AF=4,DC=5,求EF的长.24. 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)、求证:△BED≌△CFD.(2)、若∠EAC=45°,AF=4,DC=5,求EF的长.24. 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.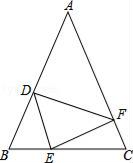 (1)、求证:△DEF是等腰三角形;(2)、当∠A=50°时,求∠DEF的度数;(3)、若∠A=∠DEF,判断△DEF是否为等腰直角三角形.25. 阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化到△ADF中即可判断.
(1)、求证:△DEF是等腰三角形;(2)、当∠A=50°时,求∠DEF的度数;(3)、若∠A=∠DEF,判断△DEF是否为等腰直角三角形.25. 阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化到△ADF中即可判断.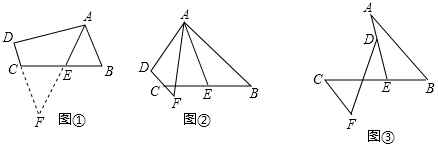
(1)、AB、AD、DC之间的等量关系为;(2)、完成(1)的证明.问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.