江苏省扬州市邵樊片2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2018-11-14 类型:期中考试
一、单选题
-
1. 下列都是同学们喜欢的商标,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在实数 中,无理数有( )A、1 B、2 C、3 D、43. 一等腰三角形的两边长分别为4和8,则这个等腰三角形的周长为( )A、16 B、20 C、18 D、16或204. 下列是勾股数的是( )A、12,15,18 B、6,10,7 C、
2. 在实数 中,无理数有( )A、1 B、2 C、3 D、43. 一等腰三角形的两边长分别为4和8,则这个等腰三角形的周长为( )A、16 B、20 C、18 D、16或204. 下列是勾股数的是( )A、12,15,18 B、6,10,7 C、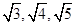 D、11,60,61
5. 如图,在△ABC中,BC=8,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长为18,则AC的长等于( )
D、11,60,61
5. 如图,在△ABC中,BC=8,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长为18,则AC的长等于( )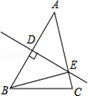 A、6 B、8 C、10 D、126. 如图,在Rt△ABC中,∠ACB=90°,CD是高,AC=4,BC=3,则线段CD的长为( )
A、6 B、8 C、10 D、126. 如图,在Rt△ABC中,∠ACB=90°,CD是高,AC=4,BC=3,则线段CD的长为( ) A、5 B、
A、5 B、 C、
C、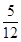 D、
D、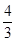 7.
7.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
 A、M点 B、N点 C、P点 D、Q点8. 如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
A、M点 B、N点 C、P点 D、Q点8. 如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )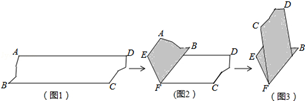 A、120° B、108° C、126° D、114°
A、120° B、108° C、126° D、114°二、填空题
-
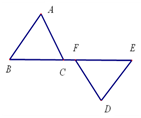
9. 已知△ABC≌△FED,∠A=20°,∠B=80°,则∠D=.10. 某市今年参加中考的学生人数大约 人,这个近似数精确到位.11. 如图,∠ACB=∠DFE,BC=EF,可以补充一个直接条件 , 就能使△ABC≌△DEF.
 12. 若一个正数的平方根分别是 和 ,则这个数是13. 一个等腰三角形的一个内角为50°,这个等腰三角形的一条腰上的高与底边的夹角是.14. 如图所示,在△ABC中,∠C=90°,AD平分∠CAB,AC=8 cm,AD=10cm,那么D点到直线AB的距离是cm.
12. 若一个正数的平方根分别是 和 ,则这个数是13. 一个等腰三角形的一个内角为50°,这个等腰三角形的一条腰上的高与底边的夹角是.14. 如图所示,在△ABC中,∠C=90°,AD平分∠CAB,AC=8 cm,AD=10cm,那么D点到直线AB的距离是cm.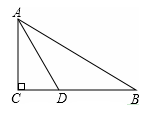 15. 如图所示,△ABC中,BA=5,BC=10,∠ABC的角平分线上有一点D,DE⊥AC于点E且AE=EC,DF⊥BC于点F,则CF=.
15. 如图所示,△ABC中,BA=5,BC=10,∠ABC的角平分线上有一点D,DE⊥AC于点E且AE=EC,DF⊥BC于点F,则CF=.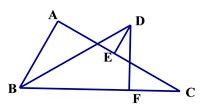 16. 如图,∠MON=90°,已知△ABC中,AC=BC=25,AB=14,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为.
16. 如图,∠MON=90°,已知△ABC中,AC=BC=25,AB=14,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为.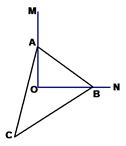
三、解答题
-
17.(1)、计算: ;(2)、求x的值:18. 已知 与 互为相反数,求x+4y的算术平方根.19. 如图所示,在边长为1个单位长度的小正方形组成的网格中,给出了格点 和 (顶点为网格线的交点),以及过格点的直线l.
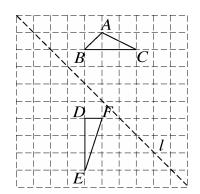 (1)、①将 向右平移3个单位长度,再向下平移1个单位长度,画出平移后的 .②画出 关于直线l对称的(2)、填空:∠C+∠E=.20. 如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE,过D作DG∥AC交BC于G.
(1)、①将 向右平移3个单位长度,再向下平移1个单位长度,画出平移后的 .②画出 关于直线l对称的(2)、填空:∠C+∠E=.20. 如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE,过D作DG∥AC交BC于G.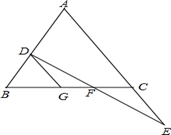
求证:
(1)、△GDF≌△CEF;(2)、△ABC是等腰三角形.21. 如图,在5×5的方格纸中,每一个小正方形的边长都为1. (1)、∠BCD是不是直角?请说明理由;(2)、求四边形ABCD的面积.22. 如图,长方形的纸片ABCD中,AD=6cm,AB=8cm,把该纸片沿直线AC折叠,点B落在点E处,AE交DC于点F.
(1)、∠BCD是不是直角?请说明理由;(2)、求四边形ABCD的面积.22. 如图,长方形的纸片ABCD中,AD=6cm,AB=8cm,把该纸片沿直线AC折叠,点B落在点E处,AE交DC于点F.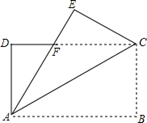 (1)、图中有等腰三角形吗?为什么?(2)、求重叠部分(即△ACF)的面积.23. 为了比较 +1与 的大小,小伍和小陆两名同学对这个问题分别进行了研究.
(1)、图中有等腰三角形吗?为什么?(2)、求重叠部分(即△ACF)的面积.23. 为了比较 +1与 的大小,小伍和小陆两名同学对这个问题分别进行了研究.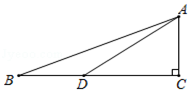 (1)、小伍同学利用计算器得到了 , ,所以确定 +1 (填“>”或“<”或“=”)(2)、小陆同学受到前面学习在数轴上用点表示无理数的启发,构造出所示的图形,其中∠C=90°,BC=3,D在BC上且BD=AC=1.请你利用此图进行计算与推理,帮小陆同学对 +1和 的大小做出准确的判断.24. 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点.
(1)、小伍同学利用计算器得到了 , ,所以确定 +1 (填“>”或“<”或“=”)(2)、小陆同学受到前面学习在数轴上用点表示无理数的启发,构造出所示的图形,其中∠C=90°,BC=3,D在BC上且BD=AC=1.请你利用此图进行计算与推理,帮小陆同学对 +1和 的大小做出准确的判断.24. 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,求证:M是BE的中点. 25. 如图
25. 如图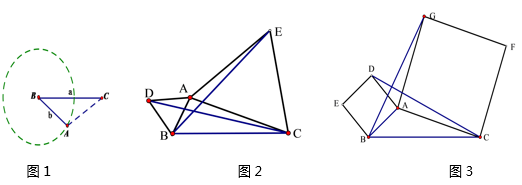 (1)、发现:如图1,点A为一动点,点B和点C 为两个定点,且BC=a,AB=b.(a>b)
(1)、发现:如图1,点A为一动点,点B和点C 为两个定点,且BC=a,AB=b.(a>b)填空:当点A位于时,线段AC的长取得最小值,且最小值为(用含a,b的式子表示)
(2)、应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最小值.
③如图3所示,分别以AB,AC为边,作正方形ADEB和正方形ACFG,连接CD,BG.写出图中线段CD,BG的关系,求线段BG的最大值
26. 如图A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.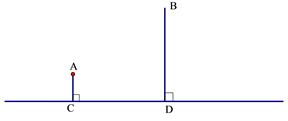 (1)、现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.
(1)、现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.方案1:水厂建在C点,修自来水管道到A村,再到B 村(即AC+AB).(如图)
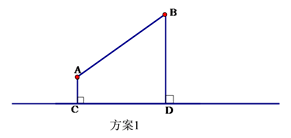
方案2:作A点关于直线CD的对称点 ,连接 交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图)
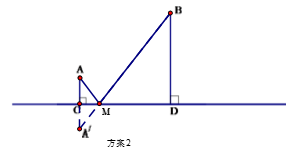
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工.请利用已有条件分别进行计算,判断哪种方案更合适.
(2)、有一艘快艇Q从这条河中驶过,当快艇Q与CD中点G相距多远时,△ABQ为等腰三角形?直接写出答案,不要说明理由.