2018-2019学年数学北师大版九年级上册第六章 反比例函数 单元测试卷
试卷更新日期:2018-09-14 类型:单元试卷
一、选择题
-
1. 如果变阻器两端电压不变,那么通过变阻器的电流 与电阻 的函数关系图象大致是( )A、
 B、
B、 C、
C、 D、
D、 2. 反比例函数 的图象上有两个点为 , ,则 与 的关系是( )A、
2. 反比例函数 的图象上有两个点为 , ,则 与 的关系是( )A、 B、
B、 C、
C、 D、不能确定
3. 如图,过 轴上任意一点 ,作 轴的平行线,分别与反比例函数 的图象交于 点和 点,若 为 轴上任意一点,连接 , ,则 的面积为( )
D、不能确定
3. 如图,过 轴上任意一点 ,作 轴的平行线,分别与反比例函数 的图象交于 点和 点,若 为 轴上任意一点,连接 , ,则 的面积为( ) A、3 B、4 C、5 D、64. 小明乘车从广州到北京,行车的平均速度y(km/h)和行车时间x(h)之间的函数图象( )A、
A、3 B、4 C、5 D、64. 小明乘车从广州到北京,行车的平均速度y(km/h)和行车时间x(h)之间的函数图象( )A、 B、
B、 C、
C、 D、
D、 5. 若反比例函数的图象经过 , ,则 ( )A、1 B、-1 C、8 D、-86. 反比例函数 的图象经过点 ,则当 时,函数值 的取值范围是( )A、
5. 若反比例函数的图象经过 , ,则 ( )A、1 B、-1 C、8 D、-86. 反比例函数 的图象经过点 ,则当 时,函数值 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 7. 点 、 、 在反比例函数 的图象上,且 ,则有( )A、
7. 点 、 、 在反比例函数 的图象上,且 ,则有( )A、 B、
B、 C、
C、 D、
D、 8. 如图,函数 和函数 的图象相交于两点,则不等式 的解集为( )
8. 如图,函数 和函数 的图象相交于两点,则不等式 的解集为( ) A、
A、 B、
B、 C、
C、 或
或  D、
D、 或
或  9. 如图,点 是反比例函数 图象上一点,过 向 轴作垂线,垂足为 ,连接 .若 的面积为 ,则 的值为( )
9. 如图,点 是反比例函数 图象上一点,过 向 轴作垂线,垂足为 ,连接 .若 的面积为 ,则 的值为( ) A、4 B、2 C、-4 D、-210. 如图,已知 是反比例函数 的图象上的一个动点, 是 轴上的一个动点,且 ,当点 在图象上自左向右运动过程中, 的面积变化情况是( )
A、4 B、2 C、-4 D、-210. 如图,已知 是反比例函数 的图象上的一个动点, 是 轴上的一个动点,且 ,当点 在图象上自左向右运动过程中, 的面积变化情况是( ) A、逐渐增大 B、逐渐减小 C、不变 D、以上都不是
A、逐渐增大 B、逐渐减小 C、不变 D、以上都不是二、填空题
-
11. 如图,矩形 的对角线 经过的坐标原点,矩形的边分别平行于坐标轴,点 在反比例函数 的图象上,若点 的坐标为 ,则 的值为 .
 12. 我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为 的滑动变阻器及一电流表测电源电压,结果如图所示.
12. 我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为 的滑动变阻器及一电流表测电源电压,结果如图所示. (1)、电流 (安培)与电阻 (欧姆)之间的函数解析式为;(2)、当电阻在 之间时,电流应在范围内,电流随电阻的增大而;(3)、若限制电流不超过 安培,则电阻在之间.13. 如图,在直角坐标系中, ,边 、 都在 轴的正半轴上,点 的坐标为 , , .反比例函数 的图象经过点 ,交 边于点 .则 的值为 .
(1)、电流 (安培)与电阻 (欧姆)之间的函数解析式为;(2)、当电阻在 之间时,电流应在范围内,电流随电阻的增大而;(3)、若限制电流不超过 安培,则电阻在之间.13. 如图,在直角坐标系中, ,边 、 都在 轴的正半轴上,点 的坐标为 , , .反比例函数 的图象经过点 ,交 边于点 .则 的值为 . 14. 如图所示,一次函数 与反比例函数 的图象相交于点 , 两点.请根据图象写出一次函数值大于反比例函数值时 的取值范围 .
14. 如图所示,一次函数 与反比例函数 的图象相交于点 , 两点.请根据图象写出一次函数值大于反比例函数值时 的取值范围 . 15. 已知y与x成正比例,z与y成反比例,则z与x成关系,当 时, ;当 时, ,则当 时, .16. 某高速公路全长为 ,那么汽车行完全程所需的时间 与行驶的平均速度 之间的关系式为 .17. 三角形面积是 ,底边为 ,高是 ,则 与 的关系式的图象位于象限.18. 反比例函数 的图象,当 时, 随 的增大而增大,则 的取值范围是 .19. 如图,已知点 、 在双曲线 上, 轴于点 , 轴于点 , 与 交于点 , 是 的中点,若 的面积为 ,则 的值等于 .
15. 已知y与x成正比例,z与y成反比例,则z与x成关系,当 时, ;当 时, ,则当 时, .16. 某高速公路全长为 ,那么汽车行完全程所需的时间 与行驶的平均速度 之间的关系式为 .17. 三角形面积是 ,底边为 ,高是 ,则 与 的关系式的图象位于象限.18. 反比例函数 的图象,当 时, 随 的增大而增大,则 的取值范围是 .19. 如图,已知点 、 在双曲线 上, 轴于点 , 轴于点 , 与 交于点 , 是 的中点,若 的面积为 ,则 的值等于 .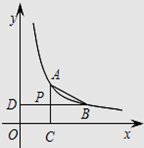 20. 如图,直线 与双曲线 交于 、 两点,若 、 两点的坐标分别为 , ,则 的值为 .
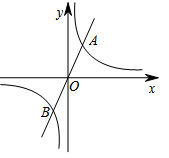
20. 如图,直线 与双曲线 交于 、 两点,若 、 两点的坐标分别为 , ,则 的值为 .
三、解答题
-
21. 已知反比例函数的图象过点 .
 (1)、这个反比例函数图象分布在哪些象限? 随 的增大而如何变化?(2)、点 , 和 哪些点在图象上?(3)、画出这个函数的图象.22. 如图,将一个∠B= 的直角三角形板的斜边 放在 轴上,直角顶点 在反比例函数 的图象上, ,求点 的坐标.
(1)、这个反比例函数图象分布在哪些象限? 随 的增大而如何变化?(2)、点 , 和 哪些点在图象上?(3)、画出这个函数的图象.22. 如图,将一个∠B= 的直角三角形板的斜边 放在 轴上,直角顶点 在反比例函数 的图象上, ,求点 的坐标.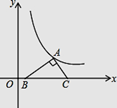 23. 如图,已知,直线 分别交 轴 轴于 、 两点, 、 的长满足 ,点 是直线 上一点,且 .
23. 如图,已知,直线 分别交 轴 轴于 、 两点, 、 的长满足 ,点 是直线 上一点,且 . (1)、求直线 的解析式;(2)、求过点 的反比例函数解析式;(3)、已知点 , 在反比例函数图象上是否存在一点 ,使以点 、 、 、 为顶点, 为腰的四边形为梯形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求直线 的解析式;(2)、求过点 的反比例函数解析式;(3)、已知点 , 在反比例函数图象上是否存在一点 ,使以点 、 、 、 为顶点, 为腰的四边形为梯形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
24. 已知反比例函数 的图象经过点 .(1)、求 的值;(2)、函数的图象在那几个象限? 随 的增大怎样变化?(3)、画出函数的图象;(4)、点 、 在这个函数的图象上吗?

