江苏省扬州市江都市五校联谊2016-2017学年七年级下学期第一次月考数学试卷

试卷更新日期：2017-03-31 类型：月考试卷

进入出卷网下载

一、选择题：

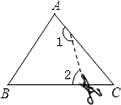
1. 下列现象是数学中的平移的是（）

A、树叶从树上落下 B、电梯从底楼升到顶楼 C、碟片在光驱中运行 D、卫星绕地球运动

查看试题解析
2. ∠1与∠2是内错角，∠1=30°，则∠2的度数为（）

A、30° B、150° C、30°或150° D、不能确定

查看试题解析
3. 下列运算正确的是（）

A、a²•a³=a⁶ B、（﹣a²）³=﹣a⁶ C、（ab）²=ab² D、a⁶÷a³=a²

查看试题解析
4. 已知三角形的两边长分别为5和7，则第三边长不可能是（）

A、1 B、3 C、5 D、7

查看试题解析
5. 若（x﹣1）⁰=1，则（）

A、x≥1 B、x≤1 C、x≠1 D、x≠0

查看试题解析
6. 如图，在△ABC中，∠C=50°，按图中虚线将∠C剪去后，∠1+∠2等于（）

A、230° B、210° C、130° D、310°

查看试题解析
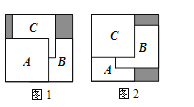
7.
把三张大小相同的正方形卡片A、B、C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示，若按图1摆放时，阴影部分的面积为S₁；若按图2摆放时，阴影部分的面积为S₂ ，则S₁与S₂的大小关系是（　　）

A、S₁＞S₂ B、S₁＜S₂ C、S₁=S₂ D、无法确定

查看试题解析
8. 如图，△ABC的面积为1．第一次操作：分别延长AB，BC，CA至点A₁ ， B₁ ， C₁ ，使A₁B=AB，B₁C=BC，C₁A=CA，顺次连接A₁ ， B₁ ， C₁ ，得到△A₁B₁C₁ ．第二次操作：分别延长A₁B₁ ， B₁C₁ ， C₁A₁至点A₂ ， B₂ ， C₂ ，使A₂B₁=A₁B₁ ， B₂C₁=B₁C₁ ， C₂A₁=C₁A₁ ，顺次连接A₂ ， B₂ ， C₂ ，得到△A₂B₂C₂ ， …按此规律，要使得到的三角形的面积超过2017，最少经过多少次操作（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题：

9. 计算（﹣2x³）³= ．

查看试题解析
10. PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为．

查看试题解析
11. 如果x+4y﹣3=0，那么2^x•16^y= ．

查看试题解析
12. 一个等腰三角形的两边长分别是3cm和7cm，则它的周长是 cm．

查看试题解析
13. 一个多边形的内角和是1800°，这个多边形是边形．

查看试题解析
14.
如图，把一副常用的三角板如图所示拼在一起，那么图中∠ABF= ．

查看试题解析
15. 如图，△ABC中，∠BAC、∠ABC、∠ACB的外角分别记为∠α，∠β，∠γ，若∠α：∠β：∠γ=3：4：5，则∠BAC：∠ABC：∠ACB等于．

查看试题解析
16.
如图，小明在操场上从A点出发，沿直线前进10米后向左转40°，再沿直线前进10米后，又向左转40°，照这样走下去，他第一次回到出发地A点时，一共走了米．

查看试题解析
17.
如图，在△ABC中E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC，△ADF，△BEF的面积分别为S_△_ABC ， S_△_ADF ， S_△_BEF ，且S_△_ABC=12，则S_△_ADF﹣S_△_BEF= ．

查看试题解析
18.
如图a是长方形纸带，∠DEF=25°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是°．

查看试题解析

三、解答题：

19. 计算：

(1)、x³•x•x²

(2)、（﹣a³）²•（﹣a²）³

(3)、|﹣2|﹣（ $\frac{2}{3}$ ）^﹣²+（π﹣3）⁰﹣（﹣1）²⁰¹⁷

(4)、（p﹣q）³•（q﹣p）⁴÷（q﹣p）² ．

查看试题解析
20. 用简便方法计算下列各题：

(1)、（ $\frac{4}{5}$ ）²⁰¹⁶×（﹣1.25）²⁰¹⁷

(2)、（2 $\frac{2}{5}$ ）¹⁰×（﹣ $\frac{5}{6}$ ）¹⁰×（ $\frac{1}{2}$ ）¹¹ ．

查看试题解析
21.
画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸中将△ABC经过一次平移后得到△A′B′C′，图中标出了点C的对应点C′．

(1)、请画出平移后的△A′B′C′；

(2)、若连接AA′，BB′，则这两条线段之间的关系是；

(3)、利用网格画出△ABC 中AC边上的中线BD；

(4)、利用网格画出△ABC 中AB边上的高CE；

(5)、△A′B′C′面积为．

查看试题解析
22. 比较大小：2¹⁰⁰与3⁷⁵（说明理由）

查看试题解析
23. 一个多边形，除一个内角外，其余各内角之和等于2012°，求这个内角的度数及多边形的边数．

查看试题解析
24.
如图，AD∥BE，AE平分∠BAD，CD与AE相交于F，∠CFE=∠E．
求证：AB∥CD．

查看试题解析
25. 如图在四边形ABCD中，∠B=∠D=90°，AE、CF分别平分∠BAD和∠BCD．试问直线AE、CF的位置关系如何？请说明你的理由．

查看试题解析
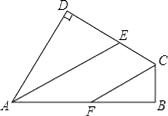26. 阅读材料：
求1+2+2²+2³+2⁴+…+2²⁰¹³的值．
解：设S=1+2+2²+2³+2⁴+…+2²⁰¹²+2²⁰¹³ ，将等式两边同时乘2，
得2S=2+2²+2³+2⁴+2⁵+…+2²⁰¹³+2²⁰¹⁴ ．
将下式减去上式，得2S﹣S=2²⁰¹⁴-1
即S=2²⁰¹⁴-1，
即1+2+2²+2³+2⁴+…+2²⁰¹³=2²⁰¹⁴-1
仿照此法计算：

(1)、1+3+3²+3³+…+3¹⁰⁰

(2)、1+ $\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}}$ +…+ $\frac{1}{2^{100}}$ ．

查看试题解析
27.
如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P=90°，PM交AB于点E，PN交CD于点F

(1)、当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为；

(2)、当△PMN所放位置如图②所示时，求证：∠PFD﹣∠AEM=90°；

(3)、在（2）的条件下，若MN与CD交于点O，且∠DON=30°，∠PEB=15°，求∠N的度数．

查看试题解析
28. 综合题。

(1)、如图①，把△ABC纸片沿DE折叠，当点A落在四边形BCED内部点A′的位置时，∠A、∠1、∠2之间有怎样的数量关系？并说明理由．

(2)、如图②，把△ABC纸片沿DE折叠，当点A落在四边形BCED外部点A′的位置时，∠A、∠1、∠2之间有怎样的数量关系？并说明理由．

(3)、如图③，把四边形ABCD沿EF折叠，当点A、D分别落在四边形BCFE内部点A′、D′的位置时，你能求出∠A′、∠D′、∠1 与∠2之间的数量关系吗？并说明理由．

查看试题解析