浙江省温州市瑞安五校2018-2019学年九年级上学期数学期中联考试卷
试卷更新日期:2018-11-30 类型:期中考试
一、选择题
-
1. 下列事件是必然事件的为( )A、明天早上会下雨 B、任意一个三角形,它的内角和等于180° C、掷一枚硬币,正面朝上 D、打开电视机,正在播放“瑞安新闻”2. 若2a=3b,则 的值为( )A、 B、 C、 D、3. 抛物线y=x2-2与y轴的交点坐标是( )A、(0,2) B、(0,-2) C、(2,0) D、(-2,0)4. 如图,以AB为直径的半圆上有一点C,∠C=25°,则∠COB的度数为( )
 A、25° B、30° C、50° D、65°5. 把抛物线 向右平移2个单位, 则所得抛物线的表达式为( )A、
A、25° B、30° C、50° D、65°5. 把抛物线 向右平移2个单位, 则所得抛物线的表达式为( )A、 B、
B、 C、
C、 D、
D、 6. 如图,直线a//b//c,直线m分别交直线a,b,c于点A,B,C,直线n分别交直线a,b,c于点D,E,F.若 ,则 的值为( )
6. 如图,直线a//b//c,直线m分别交直线a,b,c于点A,B,C,直线n分别交直线a,b,c于点D,E,F.若 ,则 的值为( ) A、
A、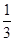 B、
B、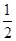 C、2
D、3
7. 如图,四边形ABCD内接于圆,∠ABC=90°,若 , 的弧长分别为3π,5π,则 的弧长为( )
C、2
D、3
7. 如图,四边形ABCD内接于圆,∠ABC=90°,若 , 的弧长分别为3π,5π,则 的弧长为( ) A、2π B、4π C、6π D、8π8. 如图,在等腰三角形ABC中,AB=AC,点D是AC的中点,若以AB为直径作圆,则下列判断正确的是( )
A、2π B、4π C、6π D、8π8. 如图,在等腰三角形ABC中,AB=AC,点D是AC的中点,若以AB为直径作圆,则下列判断正确的是( ) A、点C一定在⊙O外 B、点C一定在⊙O上 C、点D一定在⊙O外 D、点D一定在⊙O上9. 抛物线 上有点P(-1,y1)和Q(m,y2),若y1>y2 , 则m的取值范围为( )A、m>-1 B、m<-1 C、-1<m<3 D、-1≤m<310. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )
A、点C一定在⊙O外 B、点C一定在⊙O上 C、点D一定在⊙O外 D、点D一定在⊙O上9. 抛物线 上有点P(-1,y1)和Q(m,y2),若y1>y2 , 则m的取值范围为( )A、m>-1 B、m<-1 C、-1<m<3 D、-1≤m<310. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )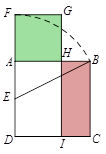 A、
A、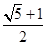 B、
B、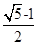 C、
D、1
C、
D、1
二、填空题
-
11. 已知线段a=1,b=4,则a,b的比例中项线段为 .12. 二次函数y=(x-1)2+2的顶点坐标为 .13. 已知扇形所在的圆半径为6cm,面积为6π cm²,则扇形圆心角的度数为 .14. 已知⊙O的半径为5,弦AB=6,M是AB上任意一点,则线段OM的最小值为 .
 15. 在直角坐标系中,抛物线y=ax2-4ax+2(a>0)交y轴于点A,点B是点A关于对称轴的对称点,点C是抛物线的顶点,若△ABC的外接圆经过原点O,则a的值为 .
15. 在直角坐标系中,抛物线y=ax2-4ax+2(a>0)交y轴于点A,点B是点A关于对称轴的对称点,点C是抛物线的顶点,若△ABC的外接圆经过原点O,则a的值为 . 16. 小明将一块长方形木板如图1所示切割,无缝隙不重叠的拼成如图2所示的“L”形状,且成轴对称图形.切割过程中木材的消耗忽略不计,若已知AB=9,BC=16,FG⊥AD则 的值为 .
16. 小明将一块长方形木板如图1所示切割,无缝隙不重叠的拼成如图2所示的“L”形状,且成轴对称图形.切割过程中木材的消耗忽略不计,若已知AB=9,BC=16,FG⊥AD则 的值为 .
三、解答题
-
17. 已知点(2,8)在函数y=ax2+b的图像上,当x=-1时,y=5.(1)、求a,b的值.(2)、如果点( ,m),(n,17)也在这个函数的图象上,求m与n的值.18. 一个布袋里装有 3 个只有颜色不同的球,其中 2 个红球,1 个白球.
 (1)、求摸出一个球是白球的概率.(2)、第一次摸出1个球,记下颜色,放回摇匀,再摸出1个球,
(1)、求摸出一个球是白球的概率.(2)、第一次摸出1个球,记下颜色,放回摇匀,再摸出1个球,求两次摸出颜色相同的球的概率(用树状图或列表来表示分
析过程).
19. 如图,A,B,C,D在⊙O上,若AC=BD,求证:BC=AD.
 20. 在6×6的方形网格中,如图所示有一个Rt△ABC,∠ACB=90°,A,B,C三点都在格点上.
20. 在6×6的方形网格中,如图所示有一个Rt△ABC,∠ACB=90°,A,B,C三点都在格点上. (1)、绕点C将△ABC顺时针旋转90°得到△A'B'C,在图甲中作出△A'B'C.(2)、以AB为边作Rt△ABD,且与Rt△ABC不全等,作出满足要求的一个点D.21. 如图,点A是二次函数y=﹣x2+2bx(b>0)图像的顶点, B(4,4),C(4,8)是线段BC的两个端点.
(1)、绕点C将△ABC顺时针旋转90°得到△A'B'C,在图甲中作出△A'B'C.(2)、以AB为边作Rt△ABD,且与Rt△ABC不全等,作出满足要求的一个点D.21. 如图,点A是二次函数y=﹣x2+2bx(b>0)图像的顶点, B(4,4),C(4,8)是线段BC的两个端点. (1)、若∠ACB=90°,求b的值.(2)、若二次函数y=-x2+2bx图像与线段BC有公共点,
(1)、若∠ACB=90°,求b的值.(2)、若二次函数y=-x2+2bx图像与线段BC有公共点,求b的取值范围.
22. 如图,AB是圆的直径,点C、D分别在AB两侧的半圆上,AC=BC,点E是BD延长线上一点,且AE∥CD. (1)、求证:△ADE是等腰直角三角形.(2)、若AB=6 ,DE=2 ,请求出CD的长.23. 某农场拟建两间矩形饲养室,一面靠现有墙(墙长足够长),中间用一道墙隔开(如图1所示).已知计划中的材料可建墙体总长46米,设两间饲养室合计长x(米),总占地面积为y(米2).
(1)、求证:△ADE是等腰直角三角形.(2)、若AB=6 ,DE=2 ,请求出CD的长.23. 某农场拟建两间矩形饲养室,一面靠现有墙(墙长足够长),中间用一道墙隔开(如图1所示).已知计划中的材料可建墙体总长46米,设两间饲养室合计长x(米),总占地面积为y(米2). (1)、求y关于x的函数表达式和自变量x的取值范围.(2)、现需要设计这两间饲养室各开一扇门(如图2所示),每扇门宽1米,门不采用计划中的材料.
(1)、求y关于x的函数表达式和自变量x的取值范围.(2)、现需要设计这两间饲养室各开一扇门(如图2所示),每扇门宽1米,门不采用计划中的材料.
①求总占地面积最大为多少米2?
②如图3所示,离墙10米外饲养室一侧准备修一条平行于墙的小路,若拟建的饲养室面积尽量大,饲养室的门口与小路的间隔为多少米?
 24. 在Rt△ABC中,∠CAB=90°,AB=8,AC=6,AD是BC边上高线.P是AB边上一动点,在CA的延长线上取一点E,使得△APE∽△ABC(点P与点B对应).过点E作EF//AD,交BC于点F,设AP=4x.
24. 在Rt△ABC中,∠CAB=90°,AB=8,AC=6,AD是BC边上高线.P是AB边上一动点,在CA的延长线上取一点E,使得△APE∽△ABC(点P与点B对应).过点E作EF//AD,交BC于点F,设AP=4x. (1)、AD= , 用x的代数式表示AE的长 .(2)、在点P的运动过程中,
(1)、AD= , 用x的代数式表示AE的长 .(2)、在点P的运动过程中,①求证:∠CEF=∠APE.
②请求出满足△PEF为等腰三角形时的所有x的值.
(3)、△BFP与△PEF的面积分别记为S1 , S2 , 点F关于直线PE的对称点记为F',若点F'落在经过B,F,P三点的圆上,请直接写出此时 的值.