人教版九年级数学上册期末检测卷
试卷更新日期:2018-12-13 类型:期末考试
一、选择题
-
1. 若反比例函数y=﹣ 的图象经过点A(3,m),则m的值是( )
A、﹣3 B、3 C、﹣ D、2. 下列图形既是轴对称图形又是中心对称图形的是( )A、 B、
B、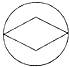 C、
C、 D、
D、 3. 下列事件中,必然发生的是( )A、某射击运动射击一次,命中靶心 B、通常情况下,水加热到100℃时沸腾 C、掷一次骰子,向上的一面是6点 D、抛一枚硬币,落地后正面朝上4. 如图,直线y=kx与双曲线y=﹣ 交于A(x1 , y1),B(x2 , y2)两点,则2x1y2﹣8x2y1的值为( )
3. 下列事件中,必然发生的是( )A、某射击运动射击一次,命中靶心 B、通常情况下,水加热到100℃时沸腾 C、掷一次骰子,向上的一面是6点 D、抛一枚硬币,落地后正面朝上4. 如图,直线y=kx与双曲线y=﹣ 交于A(x1 , y1),B(x2 , y2)两点,则2x1y2﹣8x2y1的值为( ) A、﹣6 B、﹣12 C、6 D、125. 如上图,经过原点O的⊙P与 、 轴分别交于A、B两点,点C是劣弧 上一点,则∠ACB=( )
A、﹣6 B、﹣12 C、6 D、125. 如上图,经过原点O的⊙P与 、 轴分别交于A、B两点,点C是劣弧 上一点,则∠ACB=( ) A、80° B、90° C、100° D、无法确定6.
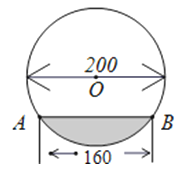
A、80° B、90° C、100° D、无法确定6.在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为( )
 A、40cm B、60cm C、80cm D、100cm7. 如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
A、40cm B、60cm C、80cm D、100cm7. 如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )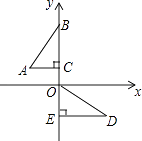 A、△ABC绕点C顺时针旋转90°,再向下平移3 B、△ABC绕点C顺时针旋转90°,再向下平移1 C、△ABC绕点C逆时针旋转90°,再向下平移1 D、△ABC绕点C逆时针旋转90°,再向下平移38. 抛物线y=(m﹣1)x2﹣mx﹣m2+1的图象过原点,则m的值为( )A、±1 B、0 C、1 D、-19. 圆的面积公式S=πR2中,S与R之间的关系是( )A、S是R的正比例函数 B、S是R的一次函数 C、S是R的二次函数 D、以上答案都不对10.
A、△ABC绕点C顺时针旋转90°,再向下平移3 B、△ABC绕点C顺时针旋转90°,再向下平移1 C、△ABC绕点C逆时针旋转90°,再向下平移1 D、△ABC绕点C逆时针旋转90°,再向下平移38. 抛物线y=(m﹣1)x2﹣mx﹣m2+1的图象过原点,则m的值为( )A、±1 B、0 C、1 D、-19. 圆的面积公式S=πR2中,S与R之间的关系是( )A、S是R的正比例函数 B、S是R的一次函数 C、S是R的二次函数 D、以上答案都不对10.如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
 A、40° B、35° C、30° D、25°11. 如图,一个大正方形中有2个小正方形,如果它们的面积分别是S1 , S2 , 则( )
A、40° B、35° C、30° D、25°11. 如图,一个大正方形中有2个小正方形,如果它们的面积分别是S1 , S2 , 则( ) A、S2>S1 B、S1=S2 C、S1>S2 D、S1≥S212. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
A、S2>S1 B、S1=S2 C、S1>S2 D、S1≥S212. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 把方程3x(x﹣2)=4(x+1)化为一元二次方程的一般形式是;
14. 小球在如图所示的地板上自由滚动,并随机地停留在某块方砖上,每一块方砖除颜色外完全相同,它最终停留在黑色方砖上的概率是 . 15. 一个侧面积为16 πcm2的圆锥,其主视图为等腰直角三角形,则这个圆锥的高为cm.16. 关于 的一元二次方程 有实数解,那么实数 的取值范围是.17.
15. 一个侧面积为16 πcm2的圆锥,其主视图为等腰直角三角形,则这个圆锥的高为cm.16. 关于 的一元二次方程 有实数解,那么实数 的取值范围是.17.如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为 .
 18. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .
18. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .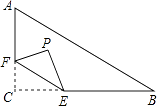
三、解答题(一)
-
19. 解方程:x2+3x﹣2=0.20. 如图为桥洞的形状,其正视图是由 和矩形ABCD构成.O点为 所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求 所在⊙O的半径DO.
 21. 如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(-1,2)
21. 如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(-1,2)
(1)画出△ABC绕点D(0,5)逆时针旋转90°后的△A1B1C1 ,
(2)写出A1 , C1的坐标.
(3)求点A旋转到A1所经过的路线长.
22. 如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .(Ⅰ)求抛物线的解析式和直线 的解析式;
(Ⅱ)当点 在线段 上运动时,求线段 的最大值;
(Ⅲ)当以 、 、 、 为顶点的四边形是平行四边形时,直接写出 的值.

四、解答题(二)
-
23. 有红、黄两个盒子,红盒子中装有编号分别为1、2、3、4的四个红球,黄盒子中装有编号为1、2、3的三个黄球.甲、乙两人玩摸球游戏,游戏规则为:甲从红盒子中每次摸出一个小球,乙从黄盒子中每次摸出一个小球,若两球编号之和为奇数,则甲胜,否则乙胜.(1)、试用列表或画树形图的方法,求甲获胜的概率;(2)、请问这个游戏规则对甲、乙双方公平吗?请说明理由.24. 如图,在平面直角坐标系xOy中,双曲线y= 与直线y=﹣2x+2交于点A(﹣1,a).
 (1)、求a,m的值;(2)、求该双曲线与直线y=﹣2x+2另一个交点B的坐标.25. 如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
(1)、求a,m的值;(2)、求该双曲线与直线y=﹣2x+2另一个交点B的坐标.25. 如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.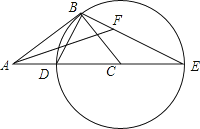 (1)、求证:△ABD∽△AEB;(2)、当 = 时,求tanE;(3)、在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.26. 如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:
(1)、求证:△ABD∽△AEB;(2)、当 = 时,求tanE;(3)、在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.26. 如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形: (1)、当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;
(1)、当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由; (2)、当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).
(2)、当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论). 27. 已知,如图①,在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
27. 已知,如图①,在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题: (1)、当t为何值时,PQ∥MN?(2)、设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(1)、当t为何值时,PQ∥MN?(2)、设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)、是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.(4)、是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.