人教版八年级数学上册期末检测卷
试卷更新日期：2018-12-13 类型：期末考试
一、选择题
-
1. 近年来，随着交通网络的不断完善，我市近郊游持续升温．据统计，在今年“五一”期间，某风景区接待游览的人数约为20.3万人，这一数据用科学记数法表示为（ ）A、20.3×104人 B、2.03×105人 C、2.03×104人 D、2.03×103人2. 下面四个交通标志图中为轴对称图形的是（ ）
A、
B、
C、
D、
3. 下列计算正确的是（ ）A、 B、 C、 D、4. 已知一个多边形的内角和为900°，则这个多边形的边数是（ ）A、6 B、7 C、8 D、95. 如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD=6，则点P到边OB的距离为（ ）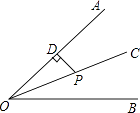
A、5 B、6 C、3 D、46. 计算（5m2+15m3n-20m4）÷（-5m2）结果正确的是（ ）A、1-3mn+4m2 B、-1-3m+4m2 C、4m2-3mn-1 D、4m2-3mn7. 如图，△ABC和△A′B′C′关于直线L对称，下列结论中正确的有（ ）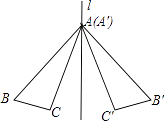
⑴△ABC≌△A′B′C′
⑵∠BAC=∠B′A′C′
⑶直线L垂直平分CC′
⑷直线BC和B′C′的交点不一定在直线L上．
A、4个 B、3个 C、2个 D、1个8. 如图，在△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=8，则CD等于（ ）
A、3 B、4 C、5 D、69. 如图，已知等腰三角形ABC，AB=AC．若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（ ）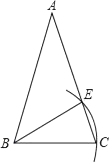
A、AE=EC B、AE=BE C、∠EBC=∠BAC D、∠EBC=∠ABE二、填空题
-
10. 若分式 有意义，则x的取值范围是 ．11. 分解因式：12. 若分式的值为0．则x= ．13. 已知一个等腰三角形的两边长分别是2和5，那么这个等腰三角形的周长为 ．14. 计算： ＝15. 如图，在等腰△ABC中，AB＝AC，∠A＝40°，线段AC的垂直平分线交AC于D，交AB于E，连接CE，则∠BCE等于.
16. 如图，AD是△ABC的中线，E、F分别是AD和AD延长线上的点，且DE=DF，连结BF、CE，下列说法：①CE=BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．
其中正确的是
三、解答题
-
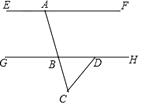
17. 化简：（ ﹣ ）÷18. 如图，直线EF∥GH，点A在EF上，AC交GH于点B，若∠FAC=72°，∠ACD=58°，点D在GH上，求∠BDC的度数．
19. 如图，在△ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于点F，且BE=CF。求证：AD平分∠BAC。
20. 如图，AD是△ABC边BC上的高，BE平分∠ABC交AD于点E．若∠C=60°，∠BED=70°．求∠ABC和∠BAC的度数．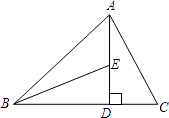
21.已知：如图，在△ABC中，AB=AC．
（1）尺规作图：作∠BAC的角平分线AD，交BC于点D．（不要求写作法，保留作图痕迹）
（2）延长AD至E点，使DE=AD，连接BE、CE．求证：四边形ABEC是菱形．
22. 某学校在商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元．
(1)、求购买一个甲种足球、一个乙种足球各需多少元？(2)、为响应“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个．恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%，如果此次购买甲、乙两种足球的总费用不超过2900元，那么这所学校最多可购买多少个乙种足球？
