2015-2016学年天津市津南区东片学区八年级下学期期中数学试卷
试卷更新日期:2017-03-30 类型:期中考试
一、选择题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 二次根式有意义的条件是( )A、x>3 B、x>﹣3 C、x≥﹣3 D、x≥33. 下列计算正确的是( )A、 B、 C、 D、4. 正方形面积为36,则对角线的长为( )A、6 B、6 C、9 D、95. 下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )A、a=1.5,b=2,c=3 B、a=7,b=24,c=25 C、a=6,b=8,c=10 D、a=3,b=4,c=56. 能判定四边形ABCD为平行四边形的题设是( )A、AB∥CD,AD=BC B、∠A=∠B,∠C=∠D C、AB=CD,AD=BC D、AB=AD,CB=CD7. 如图,在▱ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
 A、1cm B、2cm C、3cm D、4cm8. 矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )A、12 B、10 C、7.5 D、59.
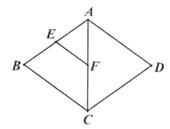
A、1cm B、2cm C、3cm D、4cm8. 矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )A、12 B、10 C、7.5 D、59.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长是( )
 A、12 B、16 C、20 D、2410. 以下条件不能判别四边形ABCD是矩形的是( )A、AB=CD,AD=BC,∠A=90° B、OA=OB=OC=OD C、AB=CD,AB∥CD,AC=BD D、AB=CD,AB∥CD,OA=OC,OB=OD11. 在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A、12 B、16 C、20 D、2410. 以下条件不能判别四边形ABCD是矩形的是( )A、AB=CD,AD=BC,∠A=90° B、OA=OB=OC=OD C、AB=CD,AB∥CD,AC=BD D、AB=CD,AB∥CD,OA=OC,OB=OD11. 在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )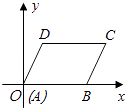 A、(3,7) B、(5,3) C、(7,3) D、(8,2)12. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
A、(3,7) B、(5,3) C、(7,3) D、(8,2)12. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( ) A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12二、填空题
-
13. = , = .14. 顺次连接矩形各边中点所得四边形为形.15. 已知菱形的两条对角线长为8和6,那么这个菱形面积是 , 菱形的高 .16. 如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,则∠AOF=度.
 17. 如图,四边形ABCD的两条对角线AC,BD互相垂直,A1 , B1 , C1 , D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为 .
17. 如图,四边形ABCD的两条对角线AC,BD互相垂直,A1 , B1 , C1 , D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为 . 18. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
18. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .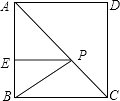
三、解答题
-
19. 计算:(1)、2 ﹣6 +3(2)、( ﹣ )÷ .20. 当x=2﹣ 时,求代数式(7+4 )x2+(2+ )x+ 的值.21. 如图所示,四边形ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求四边形ABCD的面积.
 22. 已知:如图,在矩形ABCD中,点E,F分别在AB,CD边上,BE=DF,连接CE,AF.求证:AF=CE.
22. 已知:如图,在矩形ABCD中,点E,F分别在AB,CD边上,BE=DF,连接CE,AF.求证:AF=CE. 23. 综合题。(1)、化简:2a(a+b)﹣(a+b)2(2)、如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.试判断四边形OCED的形状,并说明理由.
23. 综合题。(1)、化简:2a(a+b)﹣(a+b)2(2)、如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.试判断四边形OCED的形状,并说明理由.

