云南曲靖市2018届高三理数第一次(1月)统一检测试卷
试卷更新日期:2018-01-12 类型:高考模拟
一、单选题
-
1. 已知复数 ( 为虚数单位),则复数 在复平面内对应的点位于( )A、第四象限 B、第三象限 C、第二象限 D、第一象限2. 已知全集 ,集合 ,集合 ,那么 ( )A、
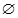 B、
B、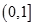 C、
C、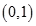 D、
D、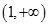 3. 计算机是将信息转换成二进制进行处理的.二进制即“缝二进一”,如 表示二进制数,将它转化成十进制形式是 ,那么将二进制数 转化成十进制形式是( )A、
3. 计算机是将信息转换成二进制进行处理的.二进制即“缝二进一”,如 表示二进制数,将它转化成十进制形式是 ,那么将二进制数 转化成十进制形式是( )A、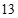 B、
B、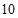 C、
C、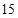 D、
D、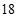 4. 若 , , ,则 , , 大小关系是( )A、
4. 若 , , ,则 , , 大小关系是( )A、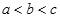 B、
B、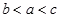 C、
C、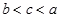 D、
D、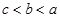 5. 已知矩形 的四个顶点的坐标分别是 , , , ,其中 两点在曲线 上,如图所示.若将一枚骰子随机放入矩形 中,则骰子落入阴影区域的概率是( )
5. 已知矩形 的四个顶点的坐标分别是 , , , ,其中 两点在曲线 上,如图所示.若将一枚骰子随机放入矩形 中,则骰子落入阴影区域的概率是( )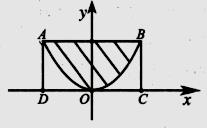 A、
A、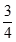 B、
B、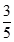 C、
C、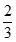 D、
D、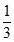 6. 下图是计算 的值的一个流程图,其中判断框内应填入的条件是( )
6. 下图是计算 的值的一个流程图,其中判断框内应填入的条件是( ) A、
A、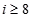 B、
B、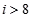 C、
C、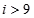 D、
D、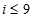 7. 如图,在 中, , ,若 ,则 ( )
7. 如图,在 中, , ,若 ,则 ( )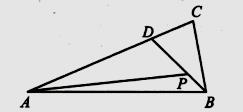 A、
A、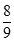 B、
B、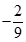 C、
C、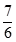 D、
D、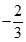 8. 已知某几何体的三视图如图所示,则该几何体的体积为( )
8. 已知某几何体的三视图如图所示,则该几何体的体积为( )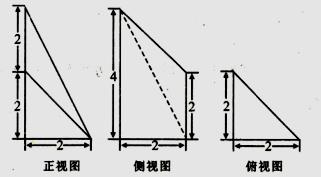 A、
A、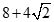 B、
B、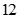 C、
C、 D、
D、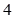 9. 数列 中, , ,设其前 项和为 ,则 ( )A、
9. 数列 中, , ,设其前 项和为 ,则 ( )A、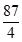 B、
B、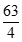 C、
C、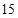 D、
D、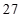 10. 的展开式中, 项的系数为 ,则 ( )A、
10. 的展开式中, 项的系数为 ,则 ( )A、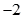 B、
B、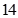 C、
C、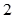 D、
D、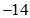 11. 在 中,内角 , , 的对边分别为 , , ,若 ,且 ,则 面积的最大值为( )A、
11. 在 中,内角 , , 的对边分别为 , , ,若 ,且 ,则 面积的最大值为( )A、 B、
B、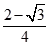 C、
C、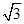 D、
D、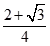 12. 设函数 ,若存在唯一的整数 ,使得 ,则 的取值范围是( )A、
12. 设函数 ,若存在唯一的整数 ,使得 ,则 的取值范围是( )A、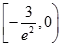 B、
B、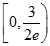 C、
C、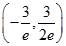 D、
D、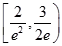
二、填空题
-
13. 随机变量 服从正态分布 ,若 ,则 .14. 实数 , 满足 ,若 的最大值为 ,则实数 的值是 .15. 抛物线 的焦点为 ,其准线与双曲线 相交于 两点,若 ,则 .16. 棱长为 的正四面体 的四个顶点都在同一个球面上,若过棱 作四面体的截面,交棱 的中点于 ,且截面面积是 ,则四面体外接球的表面积是 .
三、解答题
-
17. 若数列 是递增的等差数列,它的前 项和为 ,其中 ,且 , , 成等比数列.(1)、求 的通项公式;(2)、设 ,数列 的前 项和为 ,若对任意 , 恒成立,求 的取值范围.18. 央视传媒为了解央视举办的“朗读者”节目的收视时间情况,随机抽取了某市名 观众进行调查,其中有 名男观众和 名女观众,将这 名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在 分钟以上(包括 分钟)的称为“朗读爱好者”,收视时间在 分钟以下(不包括 分钟)的称为“非朗读爱好者”.规定只有女“朗读爱好者”可以参加央视竞选.
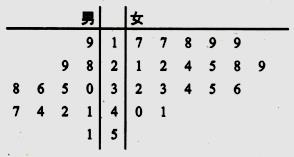 (1)、若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取 名,再从这 名观众中任选 名,求至少选到 名“朗读爱好者”的概率;(2)、若从所有的“朗读爱好者”中随机抽取 名,求抽到的 名观众中能参加央视竞选的人数 的分布列及其数学希望 .19. 如图,在三棱柱 中, 、 分别是 、 的中点.
(1)、若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取 名,再从这 名观众中任选 名,求至少选到 名“朗读爱好者”的概率;(2)、若从所有的“朗读爱好者”中随机抽取 名,求抽到的 名观众中能参加央视竞选的人数 的分布列及其数学希望 .19. 如图,在三棱柱 中, 、 分别是 、 的中点.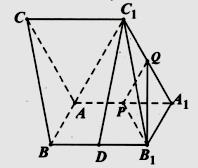 (1)、设棱 的中点为 ,证明: 平面 ;(2)、若 , , ,且平面 平面 ,求二面角 的余弦值.20. 已知椭圆 : 的离心率为 ,点 为左焦点,过点 作 轴的垂线交椭圆 于 、 两点,且 .(1)、求椭圆 的方程;(2)、在圆 上是否存在一点 ,使得在点 处的切线 与椭圆 相交于 、 两点满足 ?若存在,求 的方程;若不存在,请说明理由.
(1)、设棱 的中点为 ,证明: 平面 ;(2)、若 , , ,且平面 平面 ,求二面角 的余弦值.20. 已知椭圆 : 的离心率为 ,点 为左焦点,过点 作 轴的垂线交椭圆 于 、 两点,且 .(1)、求椭圆 的方程;(2)、在圆 上是否存在一点 ,使得在点 处的切线 与椭圆 相交于 、 两点满足 ?若存在,求 的方程;若不存在,请说明理由.