2015-2016学年山东省济宁市金乡县八年级下学期期中数学试卷

试卷更新日期：2017-03-30 类型：期中考试

进入出卷网下载

一、选择题

1. 要使二次根式 $\sqrt{5 x - 3}$ 在实数范围内有意义，则x的取值范围是（）

A、x= $\frac{3}{5}$ B、x≠ $\frac{3}{5}$ C、x≥ $\frac{3}{5}$ D、x≤ $\frac{3}{5}$

查看试题解析
2. 下列条件能判定四边形ABCD是平行四边形的是（）

A、∠A=∠B，∠C=∠D B、AB∥CD，AD=BC C、AB∥CD，∠A=∠C D、AO=BO，CO=DO

查看试题解析
3. 如图将四个全等的矩形分别等分成四个全等的小矩形，其中阴影部分面积相等的是（）

A、只有①和②相等 B、只有③和④相等 C、只有①和④相等 D、①和②，③和④分别相等

查看试题解析
4. a、b、c为△ABC三边，不是直角三角形的是（）

A、a²=c²﹣b² B、a=6，b=10，c=8 C、∠A：∠B：∠C=3：4：5 D、a=8k，b=17k，c=15k

查看试题解析
5. 若一直角三角形的两边为5和12，则它第三边的长为（）

A、13 B、 $\sqrt{119}$ C、13或 $\sqrt{129}$ D、13或 $\sqrt{119}$

查看试题解析
6. 等腰三角形底边的长为8cm，周长为18cm，则该三角形底边上的高为（）

A、6cm B、5cm C、4cm D、3cm

查看试题解析
7. 小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（）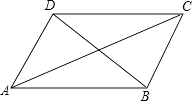

A、①② B、②③ C、①③ D、②④

查看试题解析
8. 在平静的湖面上，有一支红莲，高出水面1米，一阵风吹来，红莲移到一边，花朵齐及水面，已知红莲移动的水平距离为2米，这里的水深为（）米．

A、1.5 B、2 C、2.5 D、1

查看试题解析
9. 如图，D为△ABC内部一点，E、F两点分别在AB、BC上，且四边形DEBF为矩形，直线CD交AB于G点．若CF=6，BF=9，AG=8，则△ADC的面积为何？（）

A、16 B、24 C、36 D、54

查看试题解析
10. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是（）

A、2.5 B、 $\sqrt{5}$ C、 $\frac{3}{2} \sqrt{2}$ D、2

查看试题解析

二、填空题

11. 已知y= $\sqrt{2 x - 5}$ + $\sqrt{5 - 2 x}$ ﹣3，则2xy的值为．

查看试题解析
12. 如图，已知四边形ABCD中，AB=20cm，BC=15cm，CD=7cm，AD=24cm，∠ABC=90°．猜想∠A与∠C关系是．

查看试题解析
13. 八年级（3班）同学要在广场上布置一个矩形花坛，计划用鲜花摆成两条对角线．如果一条对角线用了20盆红花，还需要从花房运来盆红花．如果一条对角线用了25盆红花，还需要从花房运来盆红花．

查看试题解析
14. 如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3，P是AC上一动点，则PB+PE的最小值是．

查看试题解析
15.
如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进20海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD等于海里．

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{48}$ + $\sqrt{3}$ ﹣ $\sqrt{\frac{1}{2}}$ × $\sqrt{12}$ + $\sqrt{24}$

(2)、（﹣3）²﹣ $\sqrt{8}$ ﹣|1﹣2 $\sqrt{2}$ |﹣（ $\sqrt{6}$ ﹣3）⁰ ．

查看试题解析
17. 如图在8×8的正方形网格中，△ABC的顶点在边长为1的小正方形的顶点上．

(1)、填空：∠ABC= ， BC= ．

(2)、若点A在网格所在的坐标平面里的坐标为（1，﹣2），请你在图中找出一点D，写出以A、B、C、D四个点为顶点的四边形是平行四边形，在图中标出满足条件的D点位置，并直接写出D点坐标．

查看试题解析
18. 已知：如图，在△ABC中，∠B=30°，∠C=45°，AC=2 $\sqrt{2}$ ，
求：

(1)、AB的长为；

(2)、S_△_ABC= ．

查看试题解析
19. 已知：如图，在▱ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．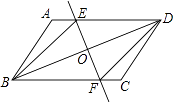

(1)、求证：△DOE≌△BOF；

(2)、当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．

查看试题解析
20. 如图，修公路遇到一座山，于是要修一条隧道．为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过C点作直线AB的垂线L，过点B作一直线（在山的旁边经过），与L相交于D点，经测量∠ABD=135°，BD=800米，求直线L上距离D点多远的C处开挖？（结果保留根号）

查看试题解析
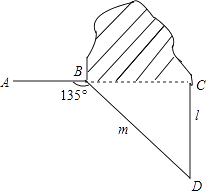21. 如图，四边形ABCD是矩形，把矩形沿AC折叠，点B落在点E处，AE与DC的交点为O，连接DE．

(1)、求证：△ADE≌△CED；

(2)、求证：DE∥AC．

查看试题解析
22.
如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE．

(1)、请判断：AF与BE的数量关系是，位置关系是；

(2)、如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予说明；

(3)、若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．

查看试题解析