2016-2017学年内蒙古赤峰市宁城县八年级上学期期末数学试卷

试卷更新日期：2017-03-30 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列多项式中能用平方差公式分解因式的是（　　）

A、a²+（﹣b）² B、5m²﹣20mn C、﹣x²﹣y² D、﹣x²+9

查看试题解析
3. 一个多边形的内角和比它的外角和的3倍少180°，这个多边形的边数是（）

A、5条 B、6条 C、7条 D、8条

查看试题解析
4. 下列运算正确的是（）

A、 $\frac{a}{a - b} - \frac{b}{b - a} = 1$ B、 $\frac{m}{a} - \frac{n}{b} = \frac{m + n}{a - b}$ C、 $\frac{b}{a} - \frac{b + 1}{a} = \frac{1}{a}$ D、 $\frac{2}{a - b} - \frac{a + b}{a^{2} - b^{2}} = \frac{1}{a - b}$

查看试题解析
5. 已知P（a，3）和Q（4，b）关于x轴对称，则（a+b）²⁰¹⁶的值为（）

A、1 B、﹣1 C、7²⁰¹⁶ D、﹣7²⁰¹⁶

查看试题解析
6. 等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（）

A、60° B、120° C、60°或150° D、60°或120°

查看试题解析
7.
如图，直线l外不重合的两点A、B，在直线l上求作一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是（）

A、转化思想 B、三角形的两边之和大于第三边 C、两点之间，线段最短 D、三角形的一个外角大于与它不相邻的任意一个内角

查看试题解析
8. 下列各式计算正确的是（）

A、x^a•x³=（x³）^a B、x^a•x³=（x^a）³ C、（x^a）⁴=（x⁴）^a D、x^a•x^a•x^a=x³⁺^a

查看试题解析
9. 若关于x的分式方程 $\frac{m - 1}{x - 1}$ =2的解为正数，则m的取值范围是（）

A、m＞﹣1 B、m≠﹣1 C、m＞1 且m≠﹣1 D、m＞﹣1且m≠1

查看试题解析
10. 如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出以下四个结论：
①AE=CF；
②△EPF是等腰直角三角形；
③S_四边形_AEPF= $\frac{1}{2}$ S_△_ABC；
④当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合） BE+CF=EF．
上述结论中始终正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题。

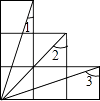
11. 因式分解：a³﹣ab²= ．

查看试题解析
12. 如图为6个边长等的正方形的组合图形，则∠1+∠2+∠3=°．

查看试题解析
13. 如图，已知△ABC的周长是22，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，△ABC的面积是．

查看试题解析
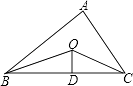14. 已知a+b=﹣3，ab=1，求a²+b²= ．

查看试题解析
15. 如图，点B在AE上，∠CAB=∠DAB，要使△ABC≌△ABD，可补充的一个条件是：．（答案不唯一，写一个即可）

查看试题解析
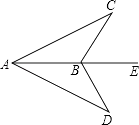16. 要使4y²+9是完全平方式，需添加一项，添加的项为（写出一个答案即可）．

查看试题解析
17. 分式 $\frac{| x | - 3}{x + 3}$ 的值为0，则x= ．

查看试题解析
18. 试在表格空白处写出下列正多边形的所有对角线条数，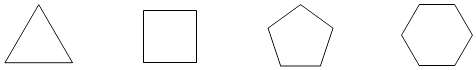
正多边形的边数
3
4
5
6
…
对角线的条数
0
2
…
根据表，猜想正n边形有条对角线．

查看试题解析

三、解答题

19. 计算：（-1）²⁰¹⁶+（π﹣3.14）⁰﹣（ $\frac{1}{2}$ ）^﹣² ．

查看试题解析
20. 化简求值：
①（2x+3y）²﹣（2x+y）•（2x﹣y），其中x= $\frac{1}{3}$ ，y=﹣ $\frac{1}{2}$
② $\frac{a^{2}}{a - 1}$ ﹣a﹣1，其中a=2．

查看试题解析
21.
平面直角坐标系中，△ABC的三个顶点坐标分别为A（0，4），B（2，4），C（3，﹣1）．

(1)、试在平面直角坐标系中，标出A、B、C三点；

(2)、求△ABC的面积．

(3)、若△A₁B₁C₁与△ABC关于x轴对称，写出A₁、B₁、C₁的坐标，并画出△A₁B₁C₁ ．

查看试题解析
22. 如图是由16个小正方形组成的正方形网格图，现已将其中的两个涂黑．请你用四种不同的方法分别在下图中再涂黑三个空白的小正方形，使它成为轴对称图形．

查看试题解析
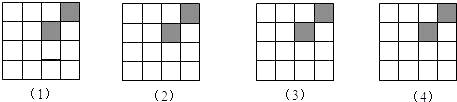23. 如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于D，CE⊥DE于E．

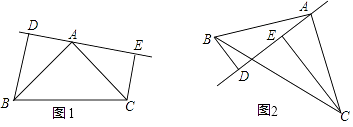(1)、若BC在DE的同侧（如图1）且AD=CE，请写出：BA和AC的位置关系．（不必证明）

(2)、若BC在DE的两侧（如图2）其他条件不变，请问（1）中AB与AC的位置关系还成立吗？若成立，写出证明过程；若不成立，说明理由．

查看试题解析
24. 京沈高铁赤峰至喀左段于2016年开工建设，天义镇路基桥墩建设初具规模，预计2019年运营，从赤峰出发经宁城至北京500公里，高铁运行速度将是现行普通客车平均速度的5倍，预计开通后，从赤峰出发，某高铁客运专列比普通客车晚3小时开出，但比普通客车早5小时到达北京，求两车的运行速度．

查看试题解析
25.
实践探究，解决问题
如图1，△ABC中，AD为BC边上的中线，则S_△_ABD=S_△_ACD ．

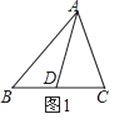(1)、
在图2中，E、F分别为矩形ABCD的边AD、BC的中点，且AB=4，AD=8，则S_阴影=；

(2)、
在图3中，E、F分别为平行四边形ABCD的边AD、BC的中点，则S_阴影和S_{平行四边形}_ABCD之间满足的关系式为；

(3)、
在图4中，E、F分别为任意四边形ABCD的边AD、BC的中点，则S_阴影和S_四边形_ABCD之间还满足（2）中的关系式吗？若满足，请予以证明，若不满足，说明理由．
解决问题：

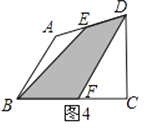(4)、
在图5中，E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点，并且图中阴影部分的面积为20平方米，求图中四个小三角形的面积和（即S₁+S₂+S₃+S₄的值）．

查看试题解析
26. 如图，已知点A、C分别在∠GBE的边BG、BE上，且AB=AC，AD∥BE，∠GBE的平分线与AD交于点D，连接CD．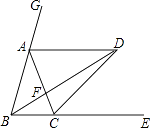

(1)、求证：①AB=AD；②CD平分∠ACE．

(2)、猜想∠BDC与∠BAC之间有何数量关系？并对你的猜想加以证明．

查看试题解析

正多边形的边数	3	4	5	6	…
对角线的条数	0	2			…