2016-2017学年北京市海淀区八年级上学期期末数学试卷
试卷更新日期:2017-03-30 类型:期末考试
一、选择题
-
1. 第24届冬季奥林匹克运动会,将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部分图形,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算中正确的是( )A、x2÷x8=x﹣4 B、a•a2=a2 C、(a3)2=a6 D、(3a)3=9a33. 石墨烯是从石墨材料中剥离出来,由碳原子组成的只有一层原子厚度的二维晶体.石墨烯(Graphene)是人类已知强度最高的物质,据科学家们测算,要施加55牛顿的压力才能使0.000001米长的石墨烯断裂.其中0.000001用科学记数法表示为( )A、1×10﹣6 B、10×10﹣7 C、0.1×10﹣5 D、1×1064. 在分式 中x的取值范围是( )A、x>﹣2 B、x<﹣2 C、x≠0 D、x≠﹣25. 下列各式中,从左到右的变形是因式分解的是( )A、2a2﹣2a+1=2a(a﹣1)+1 B、(x+y)(x﹣y)=x2﹣y2 C、x2﹣6x+5=(x﹣5)(x﹣1) D、x2+y2=(x﹣y)2+2xy6. 如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )
2. 下列运算中正确的是( )A、x2÷x8=x﹣4 B、a•a2=a2 C、(a3)2=a6 D、(3a)3=9a33. 石墨烯是从石墨材料中剥离出来,由碳原子组成的只有一层原子厚度的二维晶体.石墨烯(Graphene)是人类已知强度最高的物质,据科学家们测算,要施加55牛顿的压力才能使0.000001米长的石墨烯断裂.其中0.000001用科学记数法表示为( )A、1×10﹣6 B、10×10﹣7 C、0.1×10﹣5 D、1×1064. 在分式 中x的取值范围是( )A、x>﹣2 B、x<﹣2 C、x≠0 D、x≠﹣25. 下列各式中,从左到右的变形是因式分解的是( )A、2a2﹣2a+1=2a(a﹣1)+1 B、(x+y)(x﹣y)=x2﹣y2 C、x2﹣6x+5=(x﹣5)(x﹣1) D、x2+y2=(x﹣y)2+2xy6. 如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )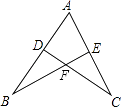 A、AD=AE B、DB=AE C、DF=EF D、DB=EC7. 下列各式中,计算正确的是( )A、(15x2y﹣5xy2)÷5xy=3x﹣5y B、98×102=(100﹣2)(100+2)=9996 C、 D、(3x+1)(x﹣2)=3x2+x﹣28.
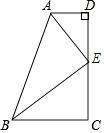
A、AD=AE B、DB=AE C、DF=EF D、DB=EC7. 下列各式中,计算正确的是( )A、(15x2y﹣5xy2)÷5xy=3x﹣5y B、98×102=(100﹣2)(100+2)=9996 C、 D、(3x+1)(x﹣2)=3x2+x﹣28.如图,∠D=∠C=90°,E是DC的中点,AE平分∠DAB,∠DEA=28°,则∠ABE的度数是( )
 A、62 B、31 C、28 D、259.
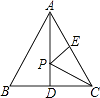
A、62 B、31 C、28 D、259.在等边三角形ABC中,D,E分别是BC,AC的中点,点P是线段AD上的一个动点,当△PCE的周长最小时,P点的位置在( )
 A、△ABC的重心处 B、AD的中点处 C、A点处 D、D点处10. 定义运算 = ,若a≠﹣1,b≠﹣1,则下列等式中不正确的是( )A、 × =1 B、 + = C、( )2= D、 =1
A、△ABC的重心处 B、AD的中点处 C、A点处 D、D点处10. 定义运算 = ,若a≠﹣1,b≠﹣1,则下列等式中不正确的是( )A、 × =1 B、 + = C、( )2= D、 =1二、填空题
-
11.
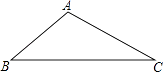
如图△ABC,在图中作出边AB上的高CD.
 12. 分解因式:x2y﹣4xy+4y= .13. 写出点M(﹣2,3)关于x轴对称的点N的坐标 .14. 如果等腰三角形的两边长分别是4、8,那么它的周长是 .15. 计算:﹣4(a2b﹣1)2÷8ab2= .16. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A=°.
12. 分解因式:x2y﹣4xy+4y= .13. 写出点M(﹣2,3)关于x轴对称的点N的坐标 .14. 如果等腰三角形的两边长分别是4、8,那么它的周长是 .15. 计算:﹣4(a2b﹣1)2÷8ab2= .16. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A=°.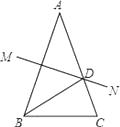 17. 教材中有如下一段文字:
17. 教材中有如下一段文字:思考
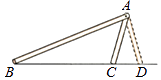
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC,固定住长木棍,转动短木棍,得到△ABD,这个实验说明了什么?
如图中的△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等.这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等.
小明通过对上述问题的再思考,提出:两边分别相等且这两边中较大边所对的角相等的两个三角形全等.请你判断小明的说法 . (填“正确”或“不正确”)
 18.
18.如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系?小明通过观察分析,形成了如下解题思路:
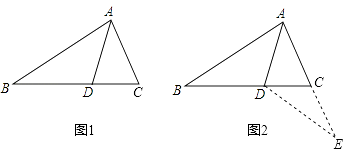
如图2,延长AC到E,使CE=CD,连接DE.由AB=AC+CD,可得AE=AB.又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB与∠ABC的数量关系.
(1)、判定△ABD与△AED全等的依据是;(2)、∠ACB与∠ABC的数量关系为: .三、解答题)
-
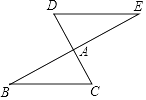
19. 分解因式:(a﹣4b)(a+b)+3ab.20. 如图,DE∥BC,点A为DC的中点,点B,A,E共线,求证:DE=CB.
 21. 解下列方程:(1)、
21. 解下列方程:(1)、= ;
(2)、﹣1= .
四、解答题
-
22. 已知a+b=2,求( + )• 的值.23. 如图,在等边三角形ABC的三边上,分别取点D,E,F,使得△DEF为等边三角形,求证:AD=BE=CF.
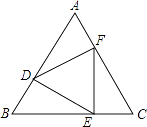 24. 列方程解应用题:
24. 列方程解应用题:老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂.”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少.
小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树.他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约千米.
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米.小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:
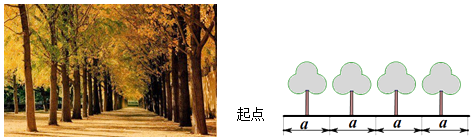
考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值.
五、解答题
-
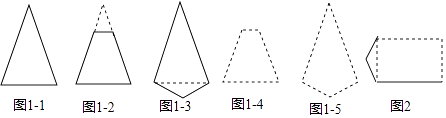
25. 在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:(1)、非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;(2)、观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,仿照类似的修改方式,请你在图1﹣4和图1﹣5中,分别修改图1﹣2和图1﹣3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;(3)、小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;(4)、
请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.
 26. 钝角三角形ABC中,∠BAC>90°,∠ACB=α,∠ABC=β,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.
26. 钝角三角形ABC中,∠BAC>90°,∠ACB=α,∠ABC=β,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE. (1)、若AB=AC,点E在AD延长线上.
(1)、若AB=AC,点E在AD延长线上.当α=30°,点D恰好为BC中点时,补全图1,直接写出∠BAE=°,
∠BEA=°;
(2)、如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);(3)、如图3,若AB<AC,∠BEA的度数与(1)中②的结论相同,直接写出∠BAE,α,β满足的数量关系.27. 一个多边形如果是轴对称图形,那么它的边数与对称轴的条数之间存在联系吗?(1)、以凸六边形为例,如果这个凸六边形是轴对称图形,那么它可能有条对称轴;(2)、凸五边形可以恰好有两条对称轴吗?如果存在请画出图形,并用虚线标出两条对称轴;否则,请说明理由;(3)、通过对(1)中凸六边形的研究,请大胆猜想,一个凸多边形如果是轴对称图形,那么它的边数与对称轴的条数之间的联系是: .