2016年黑龙江省哈尔滨市南岗区中考数学模拟试卷（五）

试卷更新日期：2017-03-30 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\frac{1}{2}$ 的相反数是（）

A、﹣2 B、2 C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下列计算正确的是（）

A、x+x²=x³ B、2x+3x=5x C、（x²）³=x⁵ D、x⁶÷x³=x²

查看试题解析
3. 下列图形中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 将二次函数y=x²﹣2x+3化为y=（x﹣h）²+k的形式，结果为（）

A、y=（x+1）²+4 B、y=（x+1）²+2 C、y=（x﹣1）²+4 D、y=（x﹣1）²+2

查看试题解析
5. 一个几何体的三视图如图所示，那么这个几何体是（）

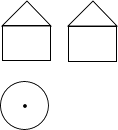A、 B、 C、 D、

查看试题解析
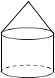6. 如图，已知经过原点的直线AB与反比例函数y= $\frac{k}{x}$ （k≠0）图象分别相交于点A和点B，过点A作AC⊥x轴于点C，若△ABC的面积为4，则k的值为（）

A、2 B、4 C、6 D、8

查看试题解析
7. 如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（）

A、 $\frac{5}{3}$ B、 $\frac{5}{2}$ C、4 D、5

查看试题解析
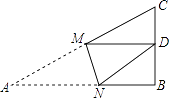8. 如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，F为BC边上一点，连接AF交DE于点G，下列说法不正确的是（）

A、 $\frac{D G}{G E} = \frac{B F}{F C}$ B、 $\frac{D G}{B F} = \frac{D E}{B C}$ C、 $\frac{A D}{D B} = \frac{B F}{F C}$ D、 $\frac{A D}{A E} = \frac{A B}{A C}$

查看试题解析
9. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠1=20°，则∠B的度数是（）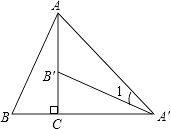

A、70° B、65° C、60° D、55°

查看试题解析
10. 如图，在平行四边形ABCD中（AB≠BC），直线EF经过其对角线的交点O，且分别交AD、BC于点M、N，交BA、DC的延长线于点E、F，下列结论：①AO=BO；②OE=OF；
③△EAM∽△EBN；④△EAO≌△CNO，其中正确的是（）

A、①② B、②③ C、②④ D、③④

查看试题解析

二、填空题

11. PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为．

查看试题解析
12. 计算 $\frac{2}{3}$ $\sqrt{\frac{1}{2}}$ ﹣ $\sqrt{8}$ = ．

查看试题解析
13. 函数y= $\frac{\sqrt{x + 2}}{x}$ 中，自变量x的取值范围是．

查看试题解析
14. 把多项式a³b﹣6a²b+9ab因式分解，最后结果等于．

查看试题解析
15. 不等式组 ${\begin{matrix} 3 x \geq x - 2 \\ \frac{x + 1}{3} > 2 x \end{matrix}$ 的解集．

查看试题解析
16. 某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人，则选出的恰为一男一女的概率是．

查看试题解析
17. 用白铁皮做罐头盒，每张铁皮可制作16个盒身或制作43个盒底，1个盒身与2个盒底配成一套罐头盒，现有150张白铁皮，用多少张制做盒身，多少张白铁皮制做盒底，可以正好制成整套罐头盒？设用x张白铁皮制做盒身，可列方程为．

查看试题解析
18. 如图，在△ABC中，以AB为直径的⊙O与AC相交于点M，弦MN∥BC，与AB相交于点E，且ME=1，AM=2，AE= $\sqrt{3}$ ，则弧BN的长为．

查看试题解析
19. 在△ABC中，AD为高线，若AB+BD=CD，AC=4 $\sqrt{5}$ ，BD=3，则线段BC的长度为．

查看试题解析
20. 菱形ABCD中，∠B=60°，延长BC至E，使得CE=BC，点F在DE上，DF=6，AG平分∠BAF，与线段BC相交于点G，若CG=2，则线段AB的长度为．

查看试题解析

三、解答题

21. 先化简，再求代数式（ $\frac{x}{x - 2}$ ﹣ $\frac{x}{x + 2}$ ）÷ $\frac{2 x}{x - 2}$ 的值，其中x=2sin45°﹣4sin30°．

查看试题解析
22. 如图，在5×8的网格中，每个小正方形的边长均为1，线段AB的顶点均在小正方形的顶点上．

(1)、画出等腰直角△ABC，点C在格点上；

(2)、画出有一个锐角的正切值是2的直角△ABD，点D在格点上；

(3)、在（1）（2）的条件下，连接CD，请直接写出△BCD的面积．

查看试题解析
23. 某校九年级举办了首届“汉字听写大赛”，全校500名九年级学生全部参加，他们同时听写50个汉字，每正确听写出一个汉字得1分，为了解学生们的成绩，随机抽取了部分学生的成绩，并根据测试成绩绘制出如下两幅不完整的统计表和频数分布直方图：
组别
成绩x分
人数
频率
1组
25≤＜30
4
0.08
2组
30≤x＜35
8
0.16
3组
35≤x＜40
a
0.32
4组
40≤x＜45
b
c
5组
45≤x＜50
10
0.2

(1)、求此次抽查了多少名学生的成绩；

(2)、通过计算将频数分布直方图补充完整；

(3)、若测试成绩不低于40分为优秀，请估计本次测试九年级学生中成绩优秀的人数．

查看试题解析
24. 在四边形ABCD中，延长CD至E，使得CE=BD，连接AE，∠ABD的角平分线与AE相交于点F．

(1)、如图1，当四边形ABCD为正方形时，连接AC交BF于G，求证：AF=FG；

(2)、如图2，当四边形ABCD为平行四边形时，判断线段AF与EF的数量关系，并证明你的判断．

查看试题解析
25. “五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．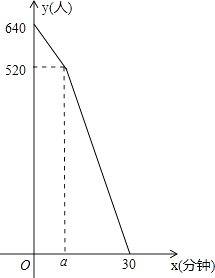

(1)、求a的值．

(2)、求检票到第20分钟时，候车室排队等候检票的旅客人数．

(3)、若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？

查看试题解析
26. 在半圆O中，AB为直径，弦AD、BC交于E，连接CD，∠C+2∠D=90°．

(1)、如图1，求证：弧AC=弧CD；

(2)、如图2，点F为劣弧BD上一点，连接OF交BC于G，连接BF，若∠CBF=45°，求证：BG=EG；

(3)、如图3，在（2）的条件下，连接AG并延长与⊙O相交于点H，连接DH，若HG=5，DH=9，求线段BE的长度．

查看试题解析
27.
抛物线y=ax（x﹣2）经过坐标原点O，与x轴相交于另外一点A，顶点B在直线y=x上；

(1)、如图1，求a值；

(2)、如图2，点C为抛物线上第四象限内一点，连接OC与对称轴相交于点D，过点C作x轴平行线，与对称轴相交于点E，与抛物线相交于点F，若BD=DE，求点C坐标；

(3)、如图3，在（2）的条件下，点M在线段OF上，连接并延长CM至点R，点N在第一象限的抛物线上，连接CN，EN，且CN=CM=RN，当∠CNR=4∠FCM时，求点N坐标．

查看试题解析
28. 下列说法正确的个数为（）个
①两组对边分别相等的四边形是平行四边形
②对角线相等的四边形是矩形
③对角线互相垂直的平行四边形是菱形
④正方形是轴对称图形，有2条对称轴．

A、1 B、2 C、3 D、4

查看试题解析
29.
如图，某数学兴趣小组在活动课上测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是1.7m，看旗杆顶部M的仰角为45°；小红的眼睛与地面的距离（CD）是1.5m，看旗杆顶部M的仰角为30°．两人相距30米且位于旗杆两侧（点B，N，D在同一条直线上）．求旗杆MN的高度．（参考数据： $\sqrt{2} \approx 1.4$ ， $\sqrt{3} \approx 1.7$ ，结果保留整数）

查看试题解析
30. 如图1，AB、CD是⊙O的弦，AB⊥CD，垂足为F，E是AB上一点，AE=CE．

(1)、延长OE与弧AC相交于点M，求证：点M是弧AC中点；

(2)、如图2，点G在AB上，连接DG，OG，延长DG，与EC相交于点H，若DG=AG．求证：∠DHC=2∠EOG；

(3)、在（2）的条件下，若∠EOG=60°，CH=2，AB=8．求CD的长．

查看试题解析

组别	成绩x分	人数	频率
1组	25≤＜30	4	0.08
2组	30≤x＜35	8	0.16
3组	35≤x＜40	a	0.32
4组	40≤x＜45	b	c
5组	45≤x＜50	10	0.2