2016-2017学年辽宁省大连市甘井子区七年级上学期期末数学试卷
试卷更新日期:2017-03-30 类型:期末考试
一、选择题:
-
1. 如图,下面几何体,从左边看到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、5a﹣3a=2 B、2a+3b=5ab C、﹣(a﹣b)=b+a D、2ab﹣ba=ab3. 解方程1﹣ ,去分母,得( )A、1﹣x﹣3=3x B、6﹣x﹣3=3x C、6﹣x+3=3x D、1﹣x+3=3x4. 小胖同学用手中一副三角尺想摆成∠α与∠β互补,下面摆放方式中符合要求的是( )A、
2. 下列运算正确的是( )A、5a﹣3a=2 B、2a+3b=5ab C、﹣(a﹣b)=b+a D、2ab﹣ba=ab3. 解方程1﹣ ,去分母,得( )A、1﹣x﹣3=3x B、6﹣x﹣3=3x C、6﹣x+3=3x D、1﹣x+3=3x4. 小胖同学用手中一副三角尺想摆成∠α与∠β互补,下面摆放方式中符合要求的是( )A、 B、
B、 C、
C、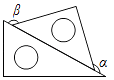 D、
D、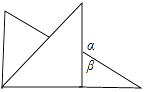 5. 若使等式(﹣4)□(﹣6)=2成立,则□中应填入的运算符号是( )A、+ B、﹣ C、× D、÷6. 下列等式变形不正确的是( )A、由x=y,得到x+2=y+2 B、由2a﹣3=b﹣3,得到2a=b C、由m=n,得到2am=2an D、由am=an,得到m=n7. 如图,有理数a、b、c、d在数轴上的对应点分别是A、B、C、D,若a、c互为相反数,则b+d( )
5. 若使等式(﹣4)□(﹣6)=2成立,则□中应填入的运算符号是( )A、+ B、﹣ C、× D、÷6. 下列等式变形不正确的是( )A、由x=y,得到x+2=y+2 B、由2a﹣3=b﹣3,得到2a=b C、由m=n,得到2am=2an D、由am=an,得到m=n7. 如图,有理数a、b、c、d在数轴上的对应点分别是A、B、C、D,若a、c互为相反数,则b+d( )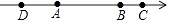 A、小于0 B、大于0 C、等于0 D、不确定
A、小于0 B、大于0 C、等于0 D、不确定二、填空题:
-
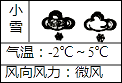
8. 比1小2的数是 .9. 如图是我市十二月份某一天的天气预报,该天最高气温比最低气温高℃.
 10. 若5xm+1y5与3x2y5是同类项,则m= .11. 如图,线段AB=10cm,点D为线段AB上一点,BD=3cm,点C为AB的中点,则线段CD的长为 cm.
10. 若5xm+1y5与3x2y5是同类项,则m= .11. 如图,线段AB=10cm,点D为线段AB上一点,BD=3cm,点C为AB的中点,则线段CD的长为 cm. 12. 如果x=1是关于x方程x+2m﹣5=0的解,则m的值是 .13.
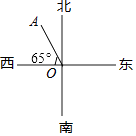
12. 如果x=1是关于x方程x+2m﹣5=0的解,则m的值是 .13.如图,点A位于点O北偏西 .
 14. 公元前1700年的古埃及纸草书中,记载着一个数学问题:“它的全部,加上它的七分之一,其和等于19.”此问题中“它”的值为 .15. 有一个数值转换器,其工作原理如图所示,若输入﹣3,则输出的结果是 .
14. 公元前1700年的古埃及纸草书中,记载着一个数学问题:“它的全部,加上它的七分之一,其和等于19.”此问题中“它”的值为 .15. 有一个数值转换器,其工作原理如图所示,若输入﹣3,则输出的结果是 .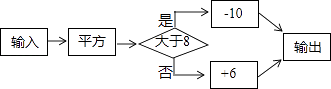
三、解答题:
-
16. 计算:(1)、12﹣(﹣18)+(﹣7)﹣15;(2)、(﹣2)3﹣(﹣3)2÷(﹣2)+(﹣3)×[(﹣4)2+2].17. 解方程:(1)、3x+7=32﹣2x(2)、3x+ =3﹣ .18. 计算:(1)、(5a2+2a﹣1)﹣4(3﹣8a+2a2);(2)、先化简,再求值:5x2+4﹣3x2﹣5x﹣2x2﹣5+6x,其中x=﹣3.19. 如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)
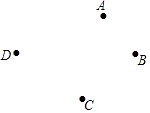 (1)、画直线AB;(2)、画射线AC;(3)、连接BC并延长BC到E,使得CE=AB+BC;(4)、在线段BD上取点P,使PA+PC的值最小.
(1)、画直线AB;(2)、画射线AC;(3)、连接BC并延长BC到E,使得CE=AB+BC;(4)、在线段BD上取点P,使PA+PC的值最小.四、解答题:
-
20. 当温度每上升1℃时,某种金属丝伸长0.002mm,反之,当温度每下降1℃时,金属丝缩短0.002mm把15℃的这种金属丝加热到60℃,再使它冷却降温到5℃,求最后的长度比原来伸长了多少?21. 已知A=3a2﹣4ab,B=a2+2ab.(1)、求A﹣2B;(2)、若|3a+1|+(2﹣3b)2=0,求A﹣2B的值.22. 某车间有22名工人,每人每天可以生产1200个螺钉或2000螺母,一个螺钉需要配两个螺母,为了使每天生产的螺钉和螺母刚好配套,则这个车间一天可最多生产多少个螺钉?
五、解答题:
-
23. 某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表所示:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)、若商场购进的甲型节能灯500只,则购买甲、乙两种节能灯共需多少元?(2)、若商场购进甲型节能灯x只,则购买甲、乙两种节能灯共需元;(用含x的代数式表示)(3)、如何进货,商场销售完节能灯时恰好获利30%,此时利润为多少元?24. 已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD. (1)、若∠COD=180°﹣α时,探索下面两个问题:
(1)、若∠COD=180°﹣α时,探索下面两个问题:①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)、如图3,当∠COD=kα,且OC在OD左侧时,直接写出∠MON的度数(用含α、k的代数式表示).25. 数学问题:如图,在数轴上点A表示的数为﹣20,点B表示的数为40,动点P从点A出发以每秒5个单位长度的速度沿正方向运动,动点Q从原点出发以每秒4个单位长度的速度沿正方向运动,动点N从点B出发以每秒8个单位的速度先沿负方向运动,到达原点后立即按原速返回,三点同时出发,当点N回到点B时,三点停止运动.
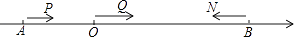 (1)、三个动点运动t(0<t<5)秒时,则P、Q、N三点在数轴上所表示的三个数分别为 , , .(2)、当QN=10个单位长度时,求此时点P在数轴上所表示的数.(3)、尝试借助上面数学问题的解题经验,建立数轴完成下面实际问题:
(1)、三个动点运动t(0<t<5)秒时,则P、Q、N三点在数轴上所表示的三个数分别为 , , .(2)、当QN=10个单位长度时,求此时点P在数轴上所表示的数.(3)、尝试借助上面数学问题的解题经验,建立数轴完成下面实际问题:码头C位于A、B两码头之间,且知AC=20海里,AB=60海里,甲船从A码头顺流驶向B码头,乙船从C码头顺流驶向B码头,丙船从B码头开往C码头后立即调头返回B码头.已知甲船在静水中航速为5海里/小时,乙船在静水中航速为4海里/小时,丙船在静水中航速为8海里/小时,水流速度为2海里/小时,三船同时出发,每艘船都行驶到B码头停止.
在整个运动过程中,是否存某一时刻,这三艘船中的一艘恰好在另外两船之间,且与两船的距离相等?若存在,请求出此时甲船离B码头的距离;若不存在,请说明理由.