2016-2017学年江西省赣州市章贡区七年级上学期期末数学试卷
试卷更新日期:2017-03-30 类型:期末考试
一、选择题
-
1. ﹣2的相反数等于( )A、 B、﹣ C、﹣2 D、2
-
2. 下列算式中,正确的是( )A、2a+3b=5ab B、3n2+2m3=5m5 C、n3﹣n2=n D、y2﹣3y2=﹣2y2
-
3. 移动互联网已经全面进入人们的日常生活,截至2016年4月,全国4G用户总数达到1.62亿,其中1.62亿用科学记数法表示为( )A、1.62×104 B、162×106 C、1.62×108 D、0.162×109
-
4. 已知x=1是一元一次方程2x﹣a=3的解,则a的值是( )A、﹣1 B、0 C、1 D、2
-
5. 如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )
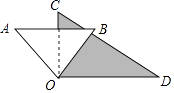 A、100° B、120° C、135° D、150°
A、100° B、120° C、135° D、150° -
6. 过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其正确展开图正确的为( )
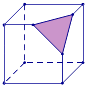 A、
A、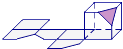 B、
B、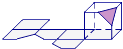 C、
C、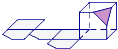 D、
D、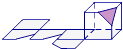
二、填空题
-
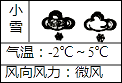
7. 如图是我市十二月份某一天的天气预报,该天最高气温比最低气温高℃.
-
8. 已知∠α的补角是它的3倍,则∠α= .
-
9. 一台电视机原价是2500元,现按原价的8折出售,则购买a台这样的电视机需要元.
-
10. 已知x2+3x=1,则多项式3x2+9x﹣1的值是 .
-
11.
用形状相同的两种菱形拼成如图所示的图案,用an表示第n个图案中菱形的个数,则an=(用含n的式子表示)

-
12. 已知有理数a,b满足ab<0,|a|>|b|,2(a+b)=|b﹣a|,则 的值为 .
三、解答题
-
13. 计算:(1)、8﹣|﹣15|+(﹣2)(2)、18﹣23+(﹣2)×3.
-
14. 解方程: +1= .
-
15.
作图题:有一张地图,图中有A,B,C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地北偏东30°方向上,在B地的南偏东45°,请你用作图的方法确定C地的位置.(保留作图痕迹,不写作法)

-
16. 化简后再求值:x+2(3y2﹣2x)﹣4(2x﹣y2),其中x=2,y=﹣1.
-
17. 有理数a、b在数轴上如图,
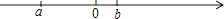 (1)、在数轴上表示﹣a、﹣b;(2)、试把这a、b、0、﹣a、﹣b五个数按从小到大用“<”连接.(3)、用>、=或<填空:|a|a,|b|b.
(1)、在数轴上表示﹣a、﹣b;(2)、试把这a、b、0、﹣a、﹣b五个数按从小到大用“<”连接.(3)、用>、=或<填空:|a|a,|b|b. -
18. 如图,当x=5.5,y=4时,求阴影部分的周长和面积.
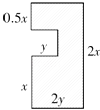
-
19. 综合题。
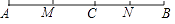 (1)、如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度.(2)、在(1)中,如果AC=acm,BC=bcm,其他条件不变,求MN的长度.
(1)、如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度.(2)、在(1)中,如果AC=acm,BC=bcm,其他条件不变,求MN的长度. -
20. 用正方形使纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成.硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
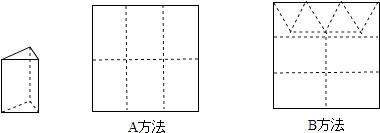 (1)、分别求裁剪出的侧面和底面的个数(用x的代数式表示)(2)、若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
(1)、分别求裁剪出的侧面和底面的个数(用x的代数式表示)(2)、若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子? -
21. 在如图所示的2017年1月份的月历表中,用一个3×2的长方形框围住相邻三列两行中的6个数字,设其中第一行中间的数字为x.
 (1)、用含x的式子表示长方形框中6个数字的和:;(2)、若长方形框中6个数字的和是141,那么这6个数字分别是哪些数字?(3)、长方形框中6个数字的和能是117吗?简要说明理由.
(1)、用含x的式子表示长方形框中6个数字的和:;(2)、若长方形框中6个数字的和是141,那么这6个数字分别是哪些数字?(3)、长方形框中6个数字的和能是117吗?简要说明理由. -
22. 如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
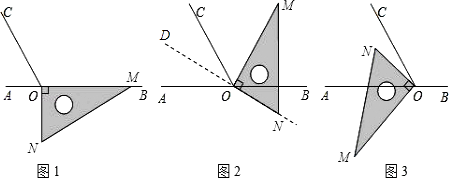 (1)、将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,设ON的反向延长线为OD,则∠COD=°,∠AOD=°.(2)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.
(1)、将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,设ON的反向延长线为OD,则∠COD=°,∠AOD=°.(2)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数. -
23. 已知式子M=(a+5)x3+7x2﹣2x+5是关于x的二次多项式,且二次多项式系数为b,数轴上A、B两点所对应的数分别是a和b.
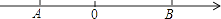 (1)、则a= , b= . A、B两点之间的距离=;(2)、有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2015次时,求点P所对应的有理数.(3)、在(2)的条件下,点P会不会在某次运动时恰好到达某一位置,使点P到点B的距离是点P到点A的距离的3倍?若可能请求出此时点P的位置,并直接指出是第几次运动,若不可能请说明理由.
(1)、则a= , b= . A、B两点之间的距离=;(2)、有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2015次时,求点P所对应的有理数.(3)、在(2)的条件下,点P会不会在某次运动时恰好到达某一位置,使点P到点B的距离是点P到点A的距离的3倍?若可能请求出此时点P的位置,并直接指出是第几次运动,若不可能请说明理由.
