人教版九年级数学上册 24.4 弧长和扇形面积（二） 同步练习
试卷更新日期：2018-09-11 类型：同步测试
一、选择题
-
1. 用圆心角为120°，半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽（如图所示），则这个纸帽的底面周长是（ ）
A、2π cm B、3π cm C、4π cm D、5π cm2. 用半径为6的半圆围成一个圆锥的侧面，则圆锥的底面半径等于（ ）A、3 B、2.5 C、2 D、1.53. 已知圆锥的侧面积为10πcm2 ， 侧面展开图的圆心角为36°，则该圆锥的母线长为（ ）A、100cm B、
cm
C、10cm
D、
cm
4. 若圆锥的底面半径为3，母线长为5，则这个圆锥的侧面积为（ ）A、6π B、8π C、15π D、30π5. 已知圆锥的底面半径为6cm，高为8cm，则圆锥的侧面积为（ ）A、 B、 C、 D、6. 如图，蒙古包可近似地看作由圆锥和圆柱组成，若用毛毡搭建一个底面圆面积为25πm2 ， 圆柱高为3m，圆锥高为2m的蒙古包，则需要毛毡的面积是（ ）
A、（30+5
）π m2
B、40π m2
C、（30+5 
）π m2
D、55π m2
7. 如图，在四边形ABCD中，AB∥CD，∠A=90°，AB=5，CD=2．以A为圆心，AD为半径的圆与BC边相切于点M，与AB交于点E，将扇形A﹣DME剪下围成一个圆锥，则圆锥的高为（ ）
A、1 B、4 C、
D、
二、填空题
-
8. 如图，圆锥的母线长为10cm，高为8cm，则该圆锥的侧面展开图（扇形）的弧长为cm．（结果用π表示）
9. 如图，从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形，将剪下的扇形围成一个圆锥，圆锥的高是m．
10. 把一个半径为16cm的圆片，剪去一个圆心角为900的扇形后，用剩下的部分做成一个圆锥的侧面，那么这个圆锥的高为.11. 用一块圆心角为 的扇形铁皮，做一个高为 的圆锥形工件（接缝忽略不计），那么这个扇形铁皮的半径是 ．12. 用一块半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则此圆锥的高为 ．13. 如图，点O为正六边形ABCDEF的中心，点M为AF中点，以点O为圆心，以OM的长为半径画弧得到扇形MON，点N在BC上；以点E为圆心，以DE的长为半径画弧得到扇形DEF，把扇形MON的两条半径OM，ON重合，围成圆锥，将此圆锥的底面半径记为r1；将扇形DEF以同样方法围成的圆锥的底面半径记为r2 ， 则r1：r2= ．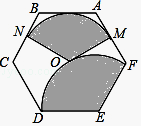
三、解答题
-
14. 如图所示，一个几何体是从高为4m，底面半径为3cm的圆柱中挖掉一个圆锥后得到的，圆锥的底面就是圆柱的上底面，圆锥的顶点在圆柱下底面的圆心上，求这个几何体的表面积．
15. 如图所示，已知圆锥的母线长AB=8cm，轴截面的顶角为60°，求圆锥全面积．
16. 一个圆锥的轴截面平行于投影面，圆锥的正投影是△ABC，已知AB＝AC＝5cm，BC＝6cm，求圆锥的体积和侧面积．17. 小明打算用一张半圆形的纸(如图)做一个圆锥．在制作过程中，他先将半圆剪成面积比为1∶2的两个扇形．
(1)、请你在图中画出他的裁剪痕迹(要求尺规作图，不写作法，保留作图痕迹)；(2)、若半圆半径是3，小明用裁出的大扇形作为圆锥的侧面，请你求出小明所做的圆锥的高．18. 如图，已知扇形 的圆心角为120º，半径为6cm.
(1)、请用尺规作出扇形的对称轴；(不写做法，保留作图痕迹)(2)、求扇形 的面积；(3)、若将此扇形围成一个圆锥的侧面(不计接缝)，求圆锥的底面圆面积.19. 如图，在△ABC中，∠ACB=90°，O是边AC上一点，以O为圆心，OA为半径的圆分别交AB，AC于点E，D，在BC的延长线上取点F，使得BF=EF，EF与AC交于点G．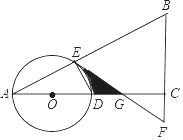
(1)、试判断直线EF与⊙O的位置关系，并说明理由；(2)、若OA=2，∠A=30°，求图中阴影部分的面积．20. 如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：
(1)、请在图中确定该圆弧所在圆心D点的位置 ， D点坐标为；(2)、连接AD、CD，求⊙D的半径及扇形DAC的圆心角度数；(3)、若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径．