湖北省襄阳市2019年初中毕业学业水平考试数学模拟卷

试卷更新日期：2018-12-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 2018的相反数是（）

A、 2018 B、-2018 C、 $\frac{1}{2018}$ D、 $\frac{- 1}{2018}$

查看试题解析
2. “厉害了，我的国！”2018年1月18日，国家统计局对外公布，全年国内生产总值（GDP）首次站上82万亿元的历史新台阶，把82万亿用科学记数法表示为（）

A、8.2×10¹³ B、8.2×10¹² C、8.2×10¹¹ D、8.2×10⁹

查看试题解析
3. 如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠ECD等于（）

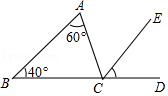A、40° B、45° C、50° D、55°

查看试题解析
4. 下列计算正确的是（）

A、7a-a=6 B、a²·a³=a⁵ C、(a³)³=a⁶ D、(ab)⁴=ab⁴

查看试题解析
5. 不等式组 ${\begin{matrix} 2 x > 1 - x \\ x + 2 < 4 x - 1 \end{matrix}$ 的解集为（）

A、x＞ $\frac{1}{3}$ B、x＞1 C、 $\frac{1}{3}$ ＜x＜1 D、空集

查看试题解析
6. 已知某物体的三视图如图所示，那么与它对应的物体是 $($ 　　 $)$

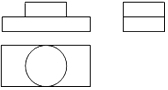A、 B、 C、 D、

查看试题解析
7. 如图，在Rt△ABC中，∠C=90°，按下列步骤作图：①以点B为圆心，适当长为半径画弧，与AB，BC分别交于点D，E；②分别以D，E为圆心，大于 $\frac{1}{2}$ DE的长为半径画弧，两弧交于点P；③作射线BP交AC于点F；④过点F作FG⊥AB于点G．下列结论正确的是（）

A、CF=FG B、AF=AG C、AF=CF D、AG=FG

查看试题解析
8. 下列语句所描述的事件是随机事件的是（）

A、任意画一个四边形，其内角和为180° B、经过任意点画一条直线 C、任意画一个菱形，是中心对称图形 D、过平面内任意三点画一个圆

查看试题解析
9. 若二次函数 $y = a x^{2} + b x + a^{2} - 2$ （ $a$ ， $b$ 为常数）的图象如图，则 $a$ 的值为（）

A、1 B、 $\sqrt{2}$ C、 $- \sqrt{2}$ D、-2

查看试题解析
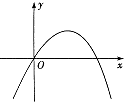10. 如图，⊙O中，半径OC⊥弦AB于点D，点E在⊙O上，∠E=22.5°，AB=4，则半径OB等于（）

A、 $\sqrt{2}$ B、2 C、2 $\sqrt{2}$ D、3

查看试题解析

二、填空题

11. 把 $\frac{2}{\sqrt{2}}$ + $\sqrt{2}$ 进行化简，得到的最简结果是（结果保留根号）．

查看试题解析
12. 计算 $\frac{5 x + 3 y}{x^{2} - y^{2}} - \frac{2 x}{x^{2} - y^{2}}$ 的结果是．

查看试题解析
13. 一个书包的标价为115元，按8折出售仍可获利15%，该书包的进价为元．

查看试题解析
14. 一组数据2，x，1，3，5，4，若这组数据的中位数是3，则这组数据的方差是．

查看试题解析
15. 已知CD是△ABC的边AB上的高，若CD= $\sqrt{3}$ ，AD=1，AB=2AC，则BC的长为．

查看试题解析
16. 折叠矩形纸片ABCD时，发现可以进行如下操作：①把△ADE翻折，点A落在DC边上的点F处，折痕为DE，点E在AB边上；②把纸片展开并铺平；③把△CDG翻折，点C落在直线AE上的点H处，折痕为DG，点G在BC边上，若AB=AD+2，EH=1，则AD=。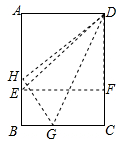

查看试题解析

三、计算题

17. 先化简，再求值：（ $\frac{x}{x y + y^{2}}$ ﹣ $\frac{y}{x^{2} + x y}$ ）÷（1﹣ $\frac{x^{2} + y^{2}}{2 x y}$ ），其中x=（ $\frac{1}{3}$ ）^﹣¹﹣（2017﹣ $\frac{3}{2}$ ）⁰ ， y= $\sqrt{3}$ sin60°．

查看试题解析

四、解答题

18. 为了计算湖中小岛上凉亭P到岸边公路l的距离，某数学兴趣小组在公路l上的点A处，测得凉亭P在北偏东60°的方向上；从A处向正东方向行走200米，到达公路l上的点B处，再次测得凉亭P在北偏东45°的方向上，如图所示．求凉亭P到公路l的距离．（结果保留整数，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析

19. 某校为了解高一年级住校生在校期间的月生活支出情况，从高一年级600名住校学生中随机抽取部分学生，对他们今年4月份的生活支出情况进行调查统计，并绘制成如下统计图表：

组别	月生活支出x（单位：元）	频数（人数）	频率
第一组	x<300	4	0.10
第二组	300≤x≤350	2	0.05
第三组	350≤x≤400	16	n
第四组	400≤x≤450	m	0.30
第五组	450≤x≤500	4	0.10
第六组	x≥500	2	0.05

请根据图表中所给的信息，解答下列问题：

(1)、在这次调查中共随机抽取了名学生，图表中的m= ， n=；

(2)、请估计该校高一年级600名住校学生今年4月份生活支出低于350元的学生人数；

(3)、现有一些爱心人士有意愿资助该校家庭困难的学生，学校在本次调查的基础上，经过进一步核实，确认高一（2）班有A，B，C三名学生家庭困难，其中A，B为女生，C为男生. 李阿姨申请资助他们中的两名，于是学校让李阿姨从A，B，C三名学生中依次随机抽取两名学生进行资助，请用列表法（或树状图法）求恰好抽到A，B两名女生的概率.

查看试题解析

20. 在某市实施城中村改造的过程中，“旺鑫”拆迁工程队承包了一项10000m²的拆迁工程．由于准备工作充分，实际拆迁效率比原计划提高了25%，提前2天完成了任务，请解答下列问题：

(1)、求“旺鑫”拆迁工程队现在平均每天拆迁多少m²；

(2)、为了尽量减少拆迁给市民带来的不便，在拆迁工作进行了2天后，“旺鑫”拆迁工程队的领导决定加快拆迁工作，将余下的拆迁任务在5天内完成，那么“旺鑫”拆迁工程队平均每天至少再多拆迁多少m²？

查看试题解析
21.
如图，一次函数 $y = k_{1} x + b$ （ $k_{1} \neq 0$ ）与反比例函数 $y = \frac{k_{2}}{x}$ （ $k_{2} \neq 0$ ）的图象交于点 $A (- 1 ， 2)$ ， $B (m ， - 1)$ ．

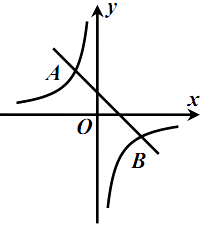(1)、求这两个函数的表达式；

(2)、在 $x$ 轴上是否存在点 $P (n ， 0)$ $(n > 0)$ ，使 $Δ A B P$ 为等腰三角形？若存在，求 $n$ 的值；若不存在，说明理由．

查看试题解析
22.
如图， $Ο$ 为 $Rt Δ Α Β C$ 的直角边 $Α C$ 上一点，以 $Ο C$ 为半径的 $⊙ Ο$ 与斜边 $Α Β$ 相切于点 $D$ ，交 $Ο Α$ 于点 $Ε$ ．已知 $Β C = \sqrt{3}$ ， $Α C = 3$ ．

(1)、求 $Α D$ 的长；

(2)、求图中阴影部分的面积．

查看试题解析

五、综合题

23. 传统的端午节即将来临，某企业接到一批粽子生产任务，约定这批粽子的出厂价为每只4元，按要求在20天内完成.为了按时完成任务，该企业招收了新工人，设新工人李明第x天生产的粽子数量为y只，y与x满足如下关系：
y= ${\begin{cases} 34 x （ 0 \leq x \leq 6 ） \\ 20 x + 80 （ 6 < x \leq 20 ） \end{cases}$

(1)、李明第几天生产的粽子数量为280只？

(2)、如图，设第x天生产的每只粽子的成本是p元，p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大？最大利润是多少元？（利润=出厂价-成本）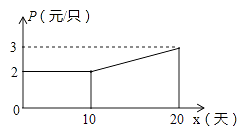

查看试题解析
24. 如图，在边长为1的正方形ABCD中，动点E、F分别在边AB、CD上，将正方形ABCD沿直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A、D重合），点C落在点N处，MN与CD交于点P，设BE=x，

(1)、当AM= $\frac{1}{3}$ 时，求x的值；

(2)、随着点M在边AD上位置的变化，△PDM的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；

(3)、设四边形BEFC的面积为S，求S与x之间的函数表达式，并求出S的最小值.

查看试题解析
25. 综合与探究
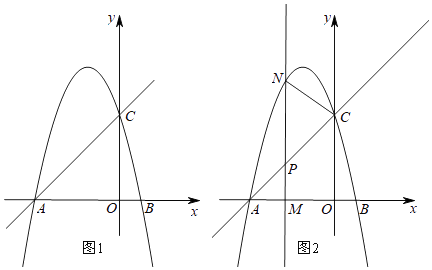
如图1所示，直线y=x+c与x轴交于点A（﹣4，0），与y轴交于点C，抛物线y=﹣x²+bx+c经过点A，C．

(1)、求抛物线的解析式

(2)、点E在抛物线的对称轴上，求CE+OE的最小值；

(3)、如图2所示，M是线段OA的上一个动点，过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N
①若以C，P，N为顶点的三角形与△APM相似，则△CPN的面积为；
②若点P恰好是线段MN的中点，点F是直线AC上一个动点，在坐标平面内是否存在点D，使以点D，F，P，M为顶点的四边形是菱形？若存在，请直接写出点D的坐标；若不存在，请说明理由．
注：二次函数y=ax²+bx +c（a≠0）的顶点坐标为（﹣ $\frac{b}{2 a}$ ， $\frac{4 a c - b^{2}}{4 a}$ ）

查看试题解析