浙教版七年级上册数学期末检测卷

试卷更新日期：2018-12-08 类型：期末考试

进入出卷网下载

一、单选题

1. 在有理数|﹣1|、（﹣1）²⁰¹⁴、﹣（﹣1）、（﹣1）²⁰¹⁵、﹣|﹣1|中负数有几个（）

A、0 B、1 C、2 D、3

查看试题解析
2. 若a^2m⁺¹b²ⁿ⁺³与5a^4m^﹣³b⁴ⁿ^﹣⁵是同类项，则m、n的值是（）

A、m=2，n=﹣2 B、m=﹣2，n=2 C、m=﹣2，n=4 D、m=2，n=4

查看试题解析
3. 如图为张小亮的答卷，他的得分应是（）

A、100分 B、80分 C、60分 D、40分

查看试题解析
4. 无理数2 $\sqrt{11}$ ﹣3在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
5. $| \sqrt{6} - 3 | + | 2 - \sqrt{6} |$ 的值为（）

A、5 B、 $5 - 2 \sqrt{6}$ C、1 D、 $2 \sqrt{6} - 1$

查看试题解析
6. 下列语句正确的有（）
①射线AB与射线BA是同一条射线②两点之间的所有连线中，线段最短③连接两点的线段叫做这两点的距离④欲将一根木条固定在墙上，至少需要2个钉子．

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，直线AB、CD相交于点O，OE平分∠BOC，OF⊥OE于O，若∠AOD=70°，则∠AOF等于（）

A、35° B、45° C、55° D、65°

查看试题解析
8. 满足 $| 2 a + 7 | + | 2 a - 1 | = 8$ 的整数 a 的个数有（）

A、9 个 B、8 个 C、5 个 D、4 个

查看试题解析
9. 如图，六位朋友均匀的围坐在圆桌旁聚会．圆桌的半径为80cm，每人离桌边10cm，又后来两位客人，每人向后挪动了相同距离并左右调整位置，使8个人都坐下，每相邻两人之间的距离与原来相邻两人之间的距离（即在圆周上两人之间的圆弧的长）相等．设每人向后挪动的距离为xcm．则根据题意，可列方程为（）

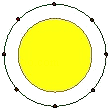A、 $\frac{60 π (80 + 10)}{180} = \frac{45 π (80 + 10 + x)}{180}$ B、 $\frac{45 π \times 80}{180} = \frac{36 π (80 + x)}{180}$ C、2π（80+10）×8=2π（80+x）×10 D、2π（80﹣x）×10=2π（80+x）×8

查看试题解析
10. 已知 $k = \frac{4 x + 3}{2 x - 1}$ ，则满足 $k$ 为整数的所有整数 $x$ 的和是（）．

A、-1 B、0 C、1 D、2

查看试题解析

二、填空题

11. 比较两个数的大小：﹣ $\frac{7}{6}$ ﹣ $\frac{8}{7}$

查看试题解析
12. 数轴上和原点的距离等于3的点表示的有理数是

查看试题解析
13. 如图，数轴上点A、B、C分别表示有理数a 、b、c ，若a 、b、c三个数的乘积为正数，这三个数的和与其中一个数相等，则b0.

查看试题解析
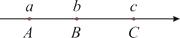14. 已知m是方程x²﹣x﹣1=0的一个根，则m（m+1）²﹣m²（m+3）+4的值为

查看试题解析
15. 如图，将三个同样的正方形的一个顶点重合放置，那么∠1的度数为．

查看试题解析
16. 某公园划船项目收费标准如下：
船型
两人船（限乘两人）
四人船（限乘四人）
六人船（限乘六人）
八人船（限乘八人）
每船租金（元/小时）
90
100
130
150
某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为元．

查看试题解析
17. 计算1+4+9+16+25+…的前29项的和是．

查看试题解析
18. 已知关于x的方程kx=5﹣x，有正整数解，则整数k的值为．

查看试题解析
19. 按一定规律排列的一列数依次为： $\frac{4}{5}$ ， $\frac{1}{2}$ ， $\frac{4}{11}$ ， $\frac{2}{7}$ ， …，按此规律，这列数中的第10个数与第16个数的积是 .

查看试题解析
20. 有这样一个数字游戏，将1，2，3，4，5，6，7，8，9这九个数字分别填在如图所示的九个空格中，要求每一行从左到右的数字逐渐增大，每一列从上到下的数字也逐渐增大．当数字3和4固定在图中所示的位置时，x代表的数字是，此时按游戏规则填写空格，所有可能出现的结果共有种．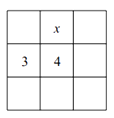

查看试题解析

三、计算题

21. 计算：

(1)、﹣20+(﹣14)﹣(﹣18)﹣13

(2)、 $4 - 8 \times {(- \frac{1}{2})}^{3}$

(3)、 $(- \frac{3}{4} - \frac{5}{9} + \frac{7}{12}) \div \frac{1}{36}$

(4)、 $| - \frac{7}{9} | \div (\frac{2}{3} - \frac{1}{5}) - \frac{1}{3} \times {(- 4)}^{2}$

查看试题解析
22. 解方程：

(1)、 $x - \frac{x - 1}{4} = 1 - \frac{3 - x}{2}$

(2)、 $1 + \frac{1 + 3 x}{4} = x - \frac{x - 1}{2}$

(3)、 $\frac{1}{2} [3 x - \frac{1}{5} (x + 1)] - 1 = x$

(4)、 $\frac{2 x + 1}{4} - 1 = \frac{2 x - 1}{3} - \frac{10 x + 1}{12}$

查看试题解析
23. 若 $x < 0$ ，化简 $\frac{| | x | - 2 x |}{| x - 3 | - | x |}$

查看试题解析

四、作图题

24. 引水渠从M向东流250米到N处，转向东北方向300米到C处，再转向北偏西30°方向，流200米到D处，试用1cm表示100米，画出相应的图形．

查看试题解析
25. 如图，已知A、B、C、D四个点．

(1)、①画直线AB、CD相交于点P；
②连接AC和BD并延长AC和BD相交于点Q；
③连接AD、BC相交于点O；

(2)、以点C为端点的射线有条；

(3)、以点C为一个端点的线段有条．

查看试题解析
26. 如图，是边长为1m的正方体，有一蜘蛛潜伏在A处，B处有一小虫被蜘蛛网粘住，请利用平面图形，画出蜘蛛爬行的最短路线．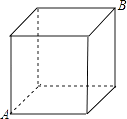

查看试题解析

五、解答题

27. 底面半径为10cm，高为40cm的圆柱形水桶中装满了水。小明先将桶中的水倒满3个底面半径为3cm，高为5cm的圆柱形杯子，如果剩下的水倒在长、宽、高分别为50cm，20cm和12cm的长方体容器内，会满出来吗？若没有满出来，求出长方体容器内水的高度（ $π$ 取3）。

查看试题解析
28. 有一个老太太提着一个篮子西瓜去卖，第一个人买走了她的西瓜的一半又半个；第二个人买走了剩下的一半又半个；第三人买走了前两个人剩下的一半又半个，正好卖完全部西瓜，问老太太一共卖了多少个西瓜．

查看试题解析
29. 在直角三角形ABC中，若AB=16cm，AC=12cm，BC=20cm．点P从点A开始以2厘米/秒的速度沿A→B→C的方向移动，点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动，如果点P、Q同时出发，用t（秒）表示移动时间，那么：

(1)、如图1，请用含t的代数式表示，①当点Q在AC上时，CQ=；
②当点Q在AB上时，AQ=；
③当点P在AB上时，BP=；④当点P在BC上时，BP= ．

(2)、如图2，若点P在线段AB上运动，点Q在线段CA上运动，当QA=AP时，试求出t的值．

(3)、如图3，当P点到达C点时，P、Q两点都停止运动，当AQ=BP时，试求出t的值．

查看试题解析

六、综合题

30. 在一个m（m≥3，m为整数）位的正整数中，若从左到右第n（n≤m，n为正整数）位上的数字与从右到左第n位上的数字之和都等于同一个常数k（k为正整数），则称这样的数为“对称等和数”．例如在正整数3186中，因为3+6=1+8=9，所以3186是“对称等和数”，其中k=9．再如在正整数53697中，因为5+7=3+9=6+6=12，所以53697是“对称等和数”，其中k=12．

(1)、已知在一个能被11整除的四位“对称等和数”中k=4．设这个四位“对称等和数”的千位上的数字为s（1≤s≤9，s为整数），百位上的数字为t（0≤t≤9，t为整数）， $\frac{s t}{2}$ 是整数，求这个四位“对称等和数”；

(2)、已知数A，数B，数C都是三位“对称等和数”．A= $\bar{1 a 5}$ （1≤a≤9，a为整数），设数B十位上的数字为x（0≤x≤9，x为整数），数C十位上的数字为y（0≤y≤9，y为整数），若A+B+C=1800，求证：y=﹣x+15．

查看试题解析

船型	两人船（限乘两人）	四人船（限乘四人）	六人船（限乘六人）	八人船（限乘八人）
每船租金（元/小时）	90	100	130	150