2016-2017学年天津市和平区九年级上学期期末数学试卷
试卷更新日期:2017-03-29 类型:期末考试
一、选择题:
-
1. 一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是( )A、摸到红球是必然事件 B、摸到白球是不可能事件 C、摸到红球比摸到白球的可能性相等 D、摸到红球比摸到白球的可能性大2. 两地的实际距离是2000m,在地图上量得这两地的距离为2cm,这幅地图的比例尺是( )A、1:1000000 B、1:100000 C、1:2000 D、1:10003. 如图,将△AOB绕点O逆时针方向旋转45°后得到△A′OB′,若∠AOB=10°,则∠AOB′的度数是( )
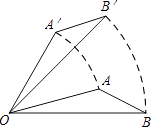 A、25° B、30° C、35° D、40°4. 对于二次函数y=2(x+1)(x﹣3),下列说法正确的是( )A、图象的开口向下 B、当x>1时,y随x的增大而减小 C、当x<1时,y随x的增大而减小 D、图象的对称轴是直线x=﹣15. 将抛物线y=x2﹣2x+2先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(﹣2,3) B、(﹣1,4) C、(3,4) D、(4,3)6. 一个不透明的袋子装有3个小球,它们除分别标有的数字1,3,5不同外,其他完全相同,任意从袋子中摸出一球后放回,再任意摸出一球,则两次摸出的球所标数字之和为6的概率是( )A、 B、 C、 D、7. 若一个正六边形的周长为24,则该正六边形的边心距为( )A、2 B、4 C、3 D、128. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则点B的对应点D的坐标为( )
A、25° B、30° C、35° D、40°4. 对于二次函数y=2(x+1)(x﹣3),下列说法正确的是( )A、图象的开口向下 B、当x>1时,y随x的增大而减小 C、当x<1时,y随x的增大而减小 D、图象的对称轴是直线x=﹣15. 将抛物线y=x2﹣2x+2先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(﹣2,3) B、(﹣1,4) C、(3,4) D、(4,3)6. 一个不透明的袋子装有3个小球,它们除分别标有的数字1,3,5不同外,其他完全相同,任意从袋子中摸出一球后放回,再任意摸出一球,则两次摸出的球所标数字之和为6的概率是( )A、 B、 C、 D、7. 若一个正六边形的周长为24,则该正六边形的边心距为( )A、2 B、4 C、3 D、128. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则点B的对应点D的坐标为( ) A、(3,3) B、(1,4) C、(3,1) D、(4,1)9. 如图,△ABC内接于⊙O,AD是∠BAC的平分线,交BC于点M,交⊙O于点D.则图中相似三角形共有( )
A、(3,3) B、(1,4) C、(3,1) D、(4,1)9. 如图,△ABC内接于⊙O,AD是∠BAC的平分线,交BC于点M,交⊙O于点D.则图中相似三角形共有( )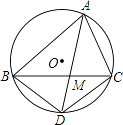 A、2对 B、4对 C、6对 D、8对10. 如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为 ,CD=4,则弦AC的长为( )
A、2对 B、4对 C、6对 D、8对10. 如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为 ,CD=4,则弦AC的长为( )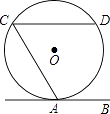 A、2 B、3 C、4 D、211. 如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为( )
A、2 B、3 C、4 D、211. 如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为( )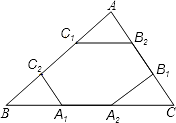 A、2I B、 I C、 I D、 I12. 如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
A、2I B、 I C、 I D、 I12. 如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( ) A、﹣3<P<﹣1 B、﹣6<P<0 C、﹣3<P<0 D、﹣6<P<﹣3
A、﹣3<P<﹣1 B、﹣6<P<0 C、﹣3<P<0 D、﹣6<P<﹣3二、填空题:
-
13. 抛物线y=ax2+bx+3经过点(2,4),则代数式4a+2b的值为 .14. 如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB、AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为 .
 15. 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=50°,则∠BAC= .
15. 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=50°,则∠BAC= .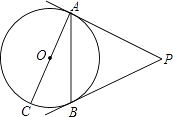 16. 一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球个数比白球个数的2倍少5个,已知从袋中摸出一个球是红球的概率是 ,则从袋中摸出一个球是白球的概率是 .17. 如图,点D、E、F分别在正三角形ABC的三边上,且△DEF也是正三角形,若△ABC的边长为a,△DEF的边长为b.则△AEF的内切圆半径为 .
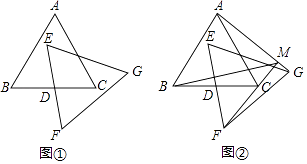
16. 一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球个数比白球个数的2倍少5个,已知从袋中摸出一个球是红球的概率是 ,则从袋中摸出一个球是白球的概率是 .17. 如图,点D、E、F分别在正三角形ABC的三边上,且△DEF也是正三角形,若△ABC的边长为a,△DEF的边长为b.则△AEF的内切圆半径为 .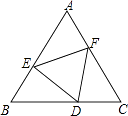 18. 已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点.
18. 已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点.(Ⅰ)如图①,这两个等边三角形的高为;
(Ⅱ)如图②,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是 .
三、解答题:
-
19. 综合题。(1)、解方程(x﹣2)(x﹣3)=0;(2)、已知关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根,求m的值取值范围.20. 已知四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OC、OA、AC.
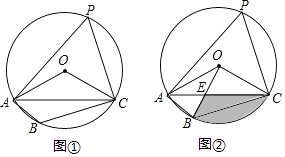 (1)、如图①,求∠OCA的度数;(2)、如图②,连接OB、OB与AC相交于点E,若∠COB=90°,OC=2 ,求BC的长和阴影部分的面积.21. 已知,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P.
(1)、如图①,求∠OCA的度数;(2)、如图②,连接OB、OB与AC相交于点E,若∠COB=90°,OC=2 ,求BC的长和阴影部分的面积.21. 已知,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P. (1)、如图①,若∠COB=2∠PCB,求证:直线PC是⊙O的切线;(2)、如图②,若点M是AB的中点,CM交AB于点N,MN•MC=36,求BM的值.22. 如图,要建一个长方形养鸡场,养鸡场的一边靠墙(墙长25米),另三边用竹篱笆围成,竹篱笆的长为40米,若要围成的养鸡场的面积为180平方米,求养鸡场的宽各为多少米,设与墙平行的一边长为x米.
(1)、如图①,若∠COB=2∠PCB,求证:直线PC是⊙O的切线;(2)、如图②,若点M是AB的中点,CM交AB于点N,MN•MC=36,求BM的值.22. 如图,要建一个长方形养鸡场,养鸡场的一边靠墙(墙长25米),另三边用竹篱笆围成,竹篱笆的长为40米,若要围成的养鸡场的面积为180平方米,求养鸡场的宽各为多少米,设与墙平行的一边长为x米.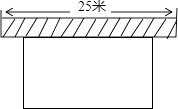 (1)、填空:(用含x的代数式表示)另一边长为米;(2)、列出方程,并求出问题的解.23. 如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)、填空:(用含x的代数式表示)另一边长为米;(2)、列出方程,并求出问题的解.23. 如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.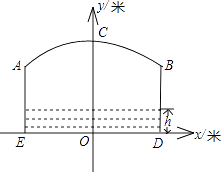 (1)、根据题意,填空:
(1)、根据题意,填空:①顶点C的坐标为;
②B点的坐标为;
(2)、求抛物线的解析式;(3)、已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h=﹣ (t﹣19)2+8(0≤t≤40),且当点C到水面的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?24.在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 .
 (1)、如图1,当点C1在线段CA的延长线时,求∠CC1A1的度数;(2)、已知AB=6,BC=8,
(1)、如图1,当点C1在线段CA的延长线时,求∠CC1A1的度数;(2)、已知AB=6,BC=8,①如图2,连接AA1 , CC1 , 若△CBC1的面积为16,求△ABA1的面积;
②如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应是点P1 , 直接写出线段EP1长度的最大值.
(3)、线段EP1长度的最大值为11,理由如下:25.将直角边长为6的等腰直角△AOC放在平面直角坐标系中,点O为坐标原点,点C、A分别在x轴,y轴的正半轴上,一条抛物线经过点A、C及点B(﹣3,0).
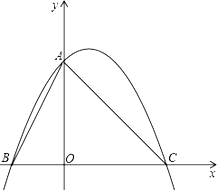 (1)、求该抛物线的解析式;(2)、若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;(3)、若点P(t,t)在抛物线上,则称点P为抛物线的不动点,将(1)中的抛物线进行平移,平移后,该抛物线只有一个不动点,且顶点在直线y=2x﹣ 上,求此时抛物线的解析式.
(1)、求该抛物线的解析式;(2)、若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;(3)、若点P(t,t)在抛物线上,则称点P为抛物线的不动点,将(1)中的抛物线进行平移,平移后,该抛物线只有一个不动点,且顶点在直线y=2x﹣ 上,求此时抛物线的解析式.