2016-2017学年山东省日照市五莲县九年级上学期期末数学试卷
试卷更新日期:2017-03-29 类型:期末考试
一、选择题
-
1. 从下列四张卡片中任取一张,卡片上的图形既是轴对称又是中心对称图形的概率是( )
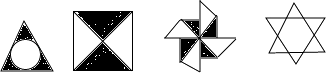 A、 B、 C、 D、12. 方程(x﹣1)(x+2)=x﹣1的解是( )A、﹣2 B、1,﹣2 C、﹣1,1 D、﹣1,33. 由二次函数y=3(x﹣4)2﹣2,可知( )A、其图象的开口向下 B、其图象的对称轴为直线x=﹣4 C、其最小值为2 D、当x<3时,y随x的增大而减小4. 二次函数y=ax2+bx+c的图象如图所示,则反比例函数 与一次函数y=bx+c在同一坐标系中的大致图象是( )
A、 B、 C、 D、12. 方程(x﹣1)(x+2)=x﹣1的解是( )A、﹣2 B、1,﹣2 C、﹣1,1 D、﹣1,33. 由二次函数y=3(x﹣4)2﹣2,可知( )A、其图象的开口向下 B、其图象的对称轴为直线x=﹣4 C、其最小值为2 D、当x<3时,y随x的增大而减小4. 二次函数y=ax2+bx+c的图象如图所示,则反比例函数 与一次函数y=bx+c在同一坐标系中的大致图象是( )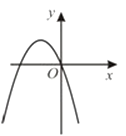 A、
A、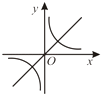 B、
B、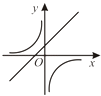 C、
C、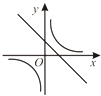 D、
D、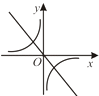 5. 如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )
5. 如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )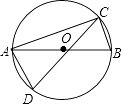 A、15° B、20° C、25° D、30°6. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )
A、15° B、20° C、25° D、30°6. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )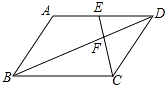 A、6 B、8 C、10 D、127. 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A、6 B、8 C、10 D、127. 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )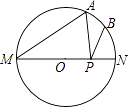 A、2 B、2 C、4 D、48. 某市2015年国内生产总值(GDP)比2014年增长了10%,由于受到国际金融危机的影响,预计2016年比2015年增长6%,若这两年GDP年平均增长率为x%,则x%满足的关系是( )A、10%+6%=x% B、(1+10%)(1+6%)=2(1+x%) C、(1+10%)(1+6%)=(1+x%)2 D、10%+6%=2•x%9. 二次函数y=x2+(2m﹣1)x+m2﹣1的图象与x轴交于点A(x1 , 0)、B(x2 , 0),且x12+x22=33,则m的值为( )A、5 B、﹣3 C、5或﹣3 D、以上都不对10. 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A、2 B、2 C、4 D、48. 某市2015年国内生产总值(GDP)比2014年增长了10%,由于受到国际金融危机的影响,预计2016年比2015年增长6%,若这两年GDP年平均增长率为x%,则x%满足的关系是( )A、10%+6%=x% B、(1+10%)(1+6%)=2(1+x%) C、(1+10%)(1+6%)=(1+x%)2 D、10%+6%=2•x%9. 二次函数y=x2+(2m﹣1)x+m2﹣1的图象与x轴交于点A(x1 , 0)、B(x2 , 0),且x12+x22=33,则m的值为( )A、5 B、﹣3 C、5或﹣3 D、以上都不对10. 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )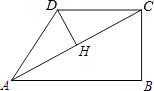 A、
A、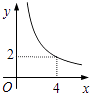 B、
B、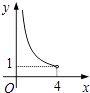 C、
C、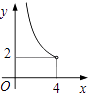 D、
D、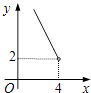 11. 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )
11. 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,给出下列结论:①∠DAC=∠ABC;②AD=CB;③点P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正确的结论是( )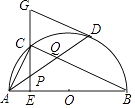 A、①③⑤ B、②④⑤ C、①②⑤ D、①③④12. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(﹣2,y1),点B( ,y2),点C( ,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( )
A、①③⑤ B、②④⑤ C、①②⑤ D、①③④12. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(﹣2,y1),点B( ,y2),点C( ,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( )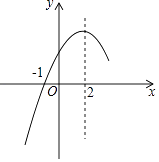 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
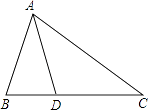
13. 如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为 .
 14. PA,PB分别切⊙O于A,B两点,点C为⊙O上不同于AB的任意一点,已知∠P=40°,则∠ACB的度数是 .
14. PA,PB分别切⊙O于A,B两点,点C为⊙O上不同于AB的任意一点,已知∠P=40°,则∠ACB的度数是 . 15. 如图,在Rt△ABC中,∠ACB=90°,AC= ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 .
15. 如图,在Rt△ABC中,∠ACB=90°,AC= ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 .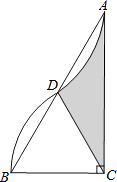 16. 如图,反比例函数y= (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为 .
16. 如图,反比例函数y= (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为 .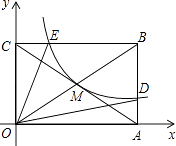
三、解答题
-
17. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
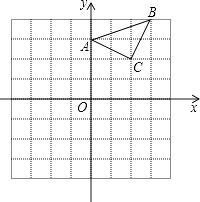 (1)、画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是;(2)、以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是;(3)、△A2B2C2的面积是平方单位.18. 某中学举行演讲比赛,经预赛,七、八年级各有一名同学进入决赛,九年级有两名同学进入决赛.(1)、请直接写出九年级同学获得第一名的概率是;(2)、用列表法或是树状图计算九年级同学获得前两名的概率.19. 某商场试销一种成本为每件50元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于40%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=60时,y=50;x=70时,y=40.(1)、求一次函数y=kx+b的表达式;(2)、若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?20. 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y= (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)、画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是;(2)、以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是;(3)、△A2B2C2的面积是平方单位.18. 某中学举行演讲比赛,经预赛,七、八年级各有一名同学进入决赛,九年级有两名同学进入决赛.(1)、请直接写出九年级同学获得第一名的概率是;(2)、用列表法或是树状图计算九年级同学获得前两名的概率.19. 某商场试销一种成本为每件50元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于40%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=60时,y=50;x=70时,y=40.(1)、求一次函数y=kx+b的表达式;(2)、若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?20. 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y= (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.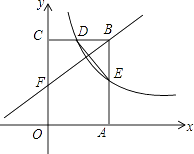 (1)、求k的值及点E的坐标;(2)、若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.21. 如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
(1)、求k的值及点E的坐标;(2)、若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.21. 如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.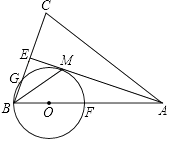 (1)、求证:AE为⊙O的切线;(2)、当BC=4,AC=6时,求⊙O的半径;(3)、在(2)的条件下,求线段BG的长.22. 如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)、求证:AE为⊙O的切线;(2)、当BC=4,AC=6时,求⊙O的半径;(3)、在(2)的条件下,求线段BG的长.22. 如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.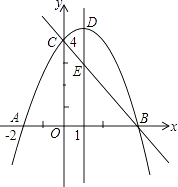 (1)、求抛物线的解析式;(2)、若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;(3)、平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
(1)、求抛物线的解析式;(2)、若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;(3)、平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.