2016-2017学年山东省临沂市兰山区九年级上学期期末数学试卷

试卷更新日期：2017-03-29 类型：期末考试

进入 出卷网 下载

一、选择题：

  • 1. sin60°的值等于（   ）
    A、12 B、2 C、3 D、32

    查看试题解析

  • 2. 为了更好地保护水资源，造福人类，某工厂计划建一个容积为200m3的污水处理池，池的底面积S（m2）与其深度h（m）满足关系式：S•h=200，则S关于h的函数图象大致是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 下列四个点，在反比例函数y= 6x 的图象上的是（   ）
    A、（﹣6，﹣1） B、（2，4） C、（3，﹣2） D、（1，﹣6）

    查看试题解析

  • 4. 下列说法正确的是（   ）
    A、为了审核书稿中的错别字，选择抽样调查 B、斜坡的坡度指的是坡角的度数 C、所有的等腰直角三角形都相似 D、“经过有交通信号灯的路口，遇到红灯”是必然事件

    查看试题解析

  • 5. 用12m长的铝材制成一个矩形窗框，使它的面积为8m2 ， 若设它的一条边长为xm，则根据题意可列出关于x的方程为（   ）

    A、x（6﹣x）=8 B、x（6+x）=8 C、x（12﹣x）=8 D、x（12﹣2x）=8

    查看试题解析

  • 6. 已知反比例函数的图象经过点P（a，﹣a），则这个函数的图象位于（   ）
    A、第一、三象限 B、第二、三象限 C、第二、四象限 D、第三、四象限

    查看试题解析

  • 7. 如图，四边形ABCD为⊙O的内接四边形，已知∠BOD=100°，则∠BCD的度数为（   ）

    A、50° B、80° C、100° D、130°

    查看试题解析

  • 8. 如图，小东用长为2.4m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为（   ）

    A、10m B、9m C、8m D、7m

    查看试题解析

  • 9. 在平面直角坐标系中，将抛物线y=x2﹣4先向右平移两个单位，再向上平移两个单位，得到的抛物线的解析式是（   ）
    A、y=（x+2）2+2 B、y=（x﹣2）2﹣2 C、y=（x﹣2）2+2 D、y=（x+2）2﹣2

    查看试题解析

  • 10. 如图，将四根长度相等的细木条首尾相接钉成四边形ABCD，当∠B=90°时，测得AC=4，改变它的形状使∠B=60°，此时AC的长度为（   ）

    A、2 B、2 C、6 D、2 2

    查看试题解析

  • 11. 已知函数y= mx 的图形如图，以下结论：

    ①m＜0；

    ②在每个分支上y随x的增大而增大；

    ③若点A（﹣1，a），点B（2，b）在图象上，则a＜b；

    ④若点P（x，y）在图象上，则点P1（﹣x，﹣y）也在图象上．其中正确的个数是（   ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 12. 一个铝质三角形框架三条边长分别为24cm、30cm、36cm，要估做一个与它相似的铝质三角形框架，现有长为27cm、45cm的两根铝材，要求以其中的一根为一边，从另一根上截下两段（允许有余料）作为另外两边．截法有（   ）
    A、0种 B、1种 C、2种 D、3种

    查看试题解析

二、填空题：

  • 13. 计算：2 2 （cos45°﹣tan60°）= ．

    查看试题解析

  • 14. 如图，若正六边形ABCDEF绕着中心点O旋转α度后得到的图形与原来图形重合，则α的最小值为°．

    查看试题解析

  • 15. 青海湖自然保护区的工作人员为了估计区内白天鹅的只数，先捕捉了30只白天鹅，并在每只白天鹅的脚上套了铁环做记号后放回；一个月后，又捕捉了100只天鹅，发现其中有脚环的白天鹅5只，据此可估算该保护区内大约有白天鹅只．

    查看试题解析

  • 16. 若抛物线y=x2+bx+1的顶点在x轴上，则b= ．

    查看试题解析

  • 17. 如图，正方形OABC与正方形ODEF是位似图形，点O为位似中心，相似比为1： 2 ，点A的坐标为（0，1），则点E的坐标是 ．

    查看试题解析

  • 18.

    如图，港口A在观测站O的正东方向，OA=6km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为 km．

    查看试题解析

三、解答题：

  • 19.

    如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2），B（1，3），△AOB绕点O逆时针旋转90°后得到△A1OB1 ．

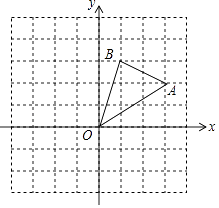    (1)、点A关于点O中心对称的点P的坐标为；

    (2)、在网格内画出△A1OB1；

    (3)、点A1、B1的坐标分别为 ．

    查看试题解析

  • 20. 如图，有一个可以自由转动的转盘被平均分成4个扇形，分别标有1、2、3、4四个数字，小王和小李各转动一次转盘为一次游戏．当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束得到一组数（若指针指在分界线时重转）．

    (1)、请你用树状图或列表的方法表示出每次游戏可能出现的所有结果；
    (2)、求每次游戏结束得到的一组数恰好是方程x2﹣4x+3=0的解的概率．

    查看试题解析

  • 21.

    如图①为一种平板电脑保护套的支架效果图，AM固定于平板电脑背面，与可活动的MB、CB部分组成支架．平板电脑的下端N保持在保护套CB上，不考虑拐角处的弧度及平板电脑和保护套的厚度，绘制成图②，其中AN表示平板电脑，M为AN上的定点，AN=CB=20cm，AM=8cm，MB=MN，我们把∠ANB叫做倾斜角，根据以上数据，判断倾斜角能小于30°吗？请说明理由．

    查看试题解析

  • 22. 已知如图，⊙O的直径AB与弦AC的夹角∠A=30°，AC=CP．

    (1)、求证：CP是⊙O的切线；
    (2)、若AB=4 3 ，求图中阴影部分的面积．

    查看试题解析

  • 23. 如图，一次函数y=kx+b与反比例函数y= 6x （x＞0）的图象交于A（m，6），B（3，n）两点．

    (1)、求一次函数的解析式；
    (2)、根据图象直接写出使kx+b＜ 6x 成立的x的取值范围；
    (3)、求△AOB的面积．

    查看试题解析

  • 24. 如图，在平行四边形ABCD中，对角线AC、BD交于点O．M为AD中点，连接CM交BD于点N，且ON=1．

    (1)、求BD的长；
    (2)、若△DCN的面积为2，求四边形ABNM的面积．

    查看试题解析

  • 25. 如图，抛物线y=ax2+bx+c的图象经过点A（﹣2，0），点B（4，0），点D（2，4），与y轴交于点C，作直线BC，连接AC、CD．

    (1)、求抛物线的函数表达式；
    (2)、E是抛物线上的点，求满足∠ECD=∠ACO的点E的坐标．

    查看试题解析