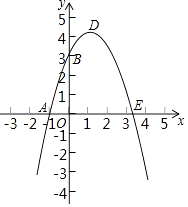2016-2017学年内蒙古巴彦淖尔市乌拉特前旗三中、四中、六中联考九年级上学期期末数学试卷
试卷更新日期:2017-03-29 类型:期末考试
一、选择题
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
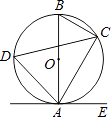
D、 2. 将函数y=﹣3x2+1的图象向右平移 个单位得到的新图象的函数解析式为( )A、 B、 C、y=﹣3x2+ D、y=﹣3x2﹣3. 如图,⊙O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为( )
2. 将函数y=﹣3x2+1的图象向右平移 个单位得到的新图象的函数解析式为( )A、 B、 C、y=﹣3x2+ D、y=﹣3x2﹣3. 如图,⊙O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为( ) A、40° B、30° C、45° D、50°4. 方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为( )A、12 B、12或15 C、15 D、不能确定5. 有6张写有数字的卡片,它们的背面都相同,现将它们背面朝上(如图),从中任意摸出一张是数字3的概率是( )
A、40° B、30° C、45° D、50°4. 方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为( )A、12 B、12或15 C、15 D、不能确定5. 有6张写有数字的卡片,它们的背面都相同,现将它们背面朝上(如图),从中任意摸出一张是数字3的概率是( )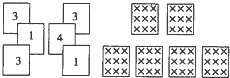 A、 B、 C、 D、6. 一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A、 B、 C、 D、6. 一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )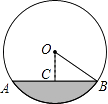 A、4 B、5 C、6 D、67. 如果矩形的面积为6,那么它的长y与宽x间的函数关系用图象表示( )A、
A、4 B、5 C、6 D、67. 如果矩形的面积为6,那么它的长y与宽x间的函数关系用图象表示( )A、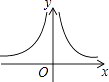 B、
B、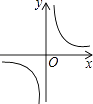 C、
C、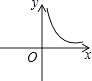 D、
D、 8. 如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
8. 如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )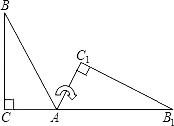 A、55° B、70° C、125° D、145°9. 一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象可能是( )A、
A、55° B、70° C、125° D、145°9. 一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象可能是( )A、 B、
B、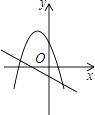 C、
C、 D、
D、 10.
10.在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2 , 设金色纸边的宽为xcm,那么x满足的方程是( )
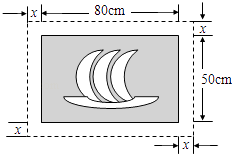 A、x2+130x﹣1400=0 B、x2+65x﹣350=0 C、x2﹣130x﹣1400=0 D、x2﹣65x﹣350=0
A、x2+130x﹣1400=0 B、x2+65x﹣350=0 C、x2﹣130x﹣1400=0 D、x2﹣65x﹣350=0二、填空题
-
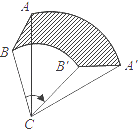
11. 方程x2=x的解是 .12. 圆内接正六边形的边长为10cm,它的边心距等于 cm.13. 在双曲线y= 上有三点A(x1 , y1),B(x2 , y2),C(x3 , y3),已知x1<x2<0<x3 , 则y1 , y2 , y3的大小关系是 . (用“<”连接)14. 已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2009的值为 .15. 如图,将△ABC绕点C旋转60°得到△A′B′C′,已知AC=6,BC=4,则线段AB扫过图形(阴影部分)的面积为 . (结果保留π)
 16. 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P=度.
16. 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,则∠P=度.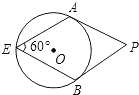 17. 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC= ,∠B=60°,则CD的长为 .
17. 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC= ,∠B=60°,则CD的长为 .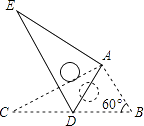 18.
18.用黑白两种颜色的正六边形地面砖按如图所示的规律,拼成若干图案:
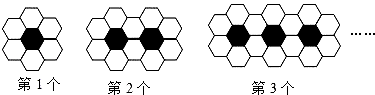 (1)、第4个图案有白色地面砖块;(2)、第n个图案有白色地面砖块.
(1)、第4个图案有白色地面砖块;(2)、第n个图案有白色地面砖块.三、解答题
-
19. 已知:如图,反比例函数y= 的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
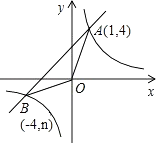 (1)、求一次函数和反比例函数的解析式;(2)、求△OAB的面积;(3)、直接写出一次函数值大于反比例函数值的自变量x的取值范围.20. 某商店购买一批单价为20元的日用品,如果以单价30元销售,那么半月内可以售出400件.据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高一元,销售量相应减少20件.如何提高销售价,才能在半月内获得最大利润?21. A、B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5.它们除了数字外没有任何区别.(1)、随机地从A中抽取一张,求抽到数字为2的概率;(2)、随机地分别从A、B中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?(3)、如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
(1)、求一次函数和反比例函数的解析式;(2)、求△OAB的面积;(3)、直接写出一次函数值大于反比例函数值的自变量x的取值范围.20. 某商店购买一批单价为20元的日用品,如果以单价30元销售,那么半月内可以售出400件.据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高一元,销售量相应减少20件.如何提高销售价,才能在半月内获得最大利润?21. A、B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5.它们除了数字外没有任何区别.(1)、随机地从A中抽取一张,求抽到数字为2的概率;(2)、随机地分别从A、B中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?(3)、如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.