广东省肇庆市封开县2018-2019中考数学模拟试卷
试卷更新日期:2018-12-07 类型:中考模拟
一、单选题
-
1. 2018的相反数是( )A、 2018 B、﹣2018 C、 D、2. 习近平主席在2018年新年贺词中指出,2017年,基本医疗保险已经覆盖1350000000人.将1350000000用科学记数法表示为( )A、135×107 B、1.35×109 C、13.5×108 D、1.35×10143. 如图,这是由5个大小相同的整体搭成的几何体,该几何体的左视图是 ( )
 A、
A、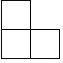 B、
B、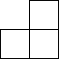 C、
C、 D、
D、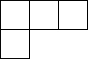 4. 某篮球运动员在连续7场比赛中的得分(单位:分)依次为20,18,23,17,20,20,18,则这组数据的众数与中位数分别是( )A、18分,17分 B、20分,17分 C、20分,19分 D、20分,20分5. 在下列图形中,既是轴对称图形又是中心对称图形的是( )A、
4. 某篮球运动员在连续7场比赛中的得分(单位:分)依次为20,18,23,17,20,20,18,则这组数据的众数与中位数分别是( )A、18分,17分 B、20分,17分 C、20分,19分 D、20分,20分5. 在下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 不等式组 的解集在数轴上表示正确的是( )
6. 不等式组 的解集在数轴上表示正确的是( )
A、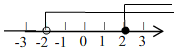 B、
B、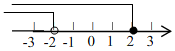 C、
C、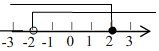 D、
D、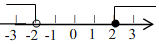 7. △ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
7. △ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A、1:2 B、1:3 C、1:4 D、1:168. 如图,点D在△ABC的边AB的延长线上,DE∥BC,若∠A=35°,∠C=24°,则∠D的度数是( )。 A、24° B、59° C、60° D、69°9. 关于x的一元二次方程(k+1)x2﹣2x+1=0有两个实数根,则k的取值范围是( )
A、24° B、59° C、60° D、69°9. 关于x的一元二次方程(k+1)x2﹣2x+1=0有两个实数根,则k的取值范围是( )
A、k≥0 B、k≤0 C、k<0且k≠﹣1 D、k≤0且k≠﹣110.如图,在矩形ABCD 中,AB=2,点E 在边AD 上,∠ABE=45°,BE=DE,连接BD,点P 在线段DE 上,过点P 作PQ∥BD 交BE 于点Q,连接QD.设PD=x,△PQD 的面积为y,则能表示y 与x 函数关系的图象大致是( )
 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
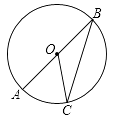
11. 如图,AB是⊙O的直径,点C为⊙O上一点,∠AOC=50°,则∠ABC= .
 12. 因式分解:2a2-2=.13. 已知 ,那么-= .
12. 因式分解:2a2-2=.13. 已知 ,那么-= .
14. 如图是一块长为a,宽为b(a>b)的长方形空地,要将阴影部分绿化,则阴影面积是. 15. 若一个正数的平方根分别为a+1和a﹣3,则这个正数为 .
15. 若一个正数的平方根分别为a+1和a﹣3,则这个正数为 .
16.如图,在平面直角坐标系中,直线l:y= x﹣ 与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 .

三、解答题(一)
-
17. 计算:|﹣4|+(﹣ )0﹣( )﹣1 .18. 先化简,再求值:( )÷ .其中a=-119. 已知:如图,Rt△ABC中,∠ACB=90°
 (1)、用直尺和圆规作∠ABC的平分线,交AC于点O;(2)、在(1)的条件下,若BC=3,AC=4,求点O到AB的距离。
(1)、用直尺和圆规作∠ABC的平分线,交AC于点O;(2)、在(1)的条件下,若BC=3,AC=4,求点O到AB的距离。四、解答题(二)
-
20. 随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
21. 为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: (1)、本次调查的学生共有人,在扇形统计图中,m的值是;(2)、将条形统计图补充完整;(3)、在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.22. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)、本次调查的学生共有人,在扇形统计图中,m的值是;(2)、将条形统计图补充完整;(3)、在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.22. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF. (1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
(1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.五、解答题(三)
-
23.
如图,已知A(﹣4,0.5),B(﹣1,2)是一次函数y=ax+b与反比例函数y=(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
 24.
24.如图,在▱ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.
(1)求证:AD=CE;
(2)判断直线BC与⊙O的位置关系,并说明理由;
(3)若BC=3,DE=6,求BE的长.
 25.
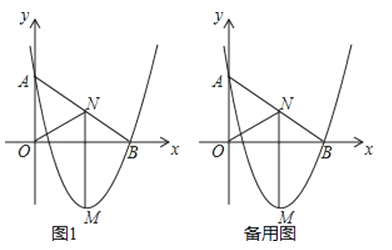
25.如图1,在平面直角坐标系中,O为坐标原点.直线y=kx+b与抛物线y=mx2﹣x+n同时经过A(0,3)、B(4,0).
(1)求m,n的值.
(2)点M是二次函数图象上一点,(点M在AB下方),过M作MN⊥x轴,与AB交于点N,与x轴交于点Q.求MN的最大值.
(3)在(2)的条件下,是否存在点N,使△AOB和△NOQ相似?若存在,求出N点坐标,不存在,说明理由.